

Review - DOI:10.33594/000000758
Accepted 12 July 2024 - Published online 19 February 2025
1Institute of Cytology, Russian Academy of Sciences, St. Petersburg, Russia,
2Department of Biological Sciences, Kent State University, Ohio, USA
The review is devoted to Alexey Vereninov's research in the field of cell permeability and ion homeostasis. Particular attention is paid to the modeling approach developed in the study of frog striated muscles and subsequently applied to other cell types. Biologically relevant ways by which the muscles were studied and the model that was constructed determines the overall nonreductionist approach of the research. In the first study of excitability in invertebrate tissues and organs Vereninov used techniques and methods derived from his teacher Dmitry Nasonov. From 1963 to 1971, he tested membrane and phase concepts of bioelectrogenesis using isolated fibers and whole sartorius muscles. Both mechanistic and theoretical models have been used in the study of “salt potentials”. The properties of muscles considered in these models are relevant to both the phase and membrane models. Vereninov’s work, therefore, led to reconciliation between the two theories. In studies performed in 1971 and 1976 Vereninov presented a nonreductionist approach to the study of ion and osmotic balance in animal cells. Using the concept of cell permeability, he developed a method to analyze potassium permeability by combining electrophysiological and ionic data. In 1980-1983 Vereninov applied Ussing's criterion to study the role of passive permeability in the ion balance of muscles in a bi-ionic system. These studies were carried out under specific ionic conditions that allow the distinction between passive and active components of ion transport. Under these conditions, sodium was actively transported, and potassium exhibited both active and passive transport. Moreover, in a bi-ionic system with rubidium and potassium, some unidentified transport component was also present. Therefore, instead of Ussing's criterion, the application of which is restricted to specific experimental conditions, the analysis of ion fluxes was carried out using mathematical modeling.
The review covers the experimental and theoretical aspects of Alexey Vereninov's work on permeability and ionic homeostasis in animal cells. The methodological aspect of his work is essential in his early studies. Vereninov’s publications between 1963 and 1983 show a wide range of scientific interests of the author. A deep knowledge of physics and mathematics allowed him to conduct physiological experiments and mathematical modeling. To resolve methodological issues Vereninov further developed a non-reductionist modeling approach inherited from his predecessors and teachers. Using muscles and later blood cells allowed him to avoid some methodological problems connected with cell isolation. Later, when studying processes at lower levels of the organization, he chose the most relevant methods that did not compromise the biological specificity of the work. Thus, in the study of cancer and apoptosis, he used a morphological method that may be considered non-reductionist in the methodological sense.
One of the first physiologists who realized the role of the cell as the basis of the most important biological processes was Dmitry Nasonov. Considering the ability of the cell to maintain constant volume, Nasonov avoided mechanistic explanations, relating it to one of specific cellular functions. At that point, the ideas of Nasonov were supported by the concept of cell permeability developed by A. Troshin [1]. Later, the topic of ionic homeostasis in animal cells became central in Vereninov’s research. However, that direction of cellular research was formed only after some time: he started with an investigation on the problem of excitability using invertebrate tissues [2]. Meanwhile, in studying neurons, he mastered electrophysiological and histological methods, including vital cell staining. Following the general trend of cellular studies, he used the sartorius muscle as a laboratory model for the study of cell permeability. Due to specifics of intracellular organization, muscles occupy an intermediate position between cells and tissues. This view was supported by experiments of S. Krolenko, who studied the functional activity of frog muscle fibers, which can be considered as a unit of muscle organization. He demonstrated that the fibers are identical to the whole muscle in regard to their electrophysiological and osmotic properties. It should be noted that nerves and muscles are considered as cells only in particular physiological contexts [3].
Vereninov and his colleagues made microelectrode impalements of muscle fibers to measure transmembrane potential (TP), while the ion content and ion fluxes were measured on the entire muscle. In this approach, electrophysiological and electrochemical parameters of the cell were associated with the phenomenon of bioelectrogenesis either by mathematical modeling or the analysis of empirical data. These studies allowed to relate the passive mechanism of membrane transport with its role in generation of TP [4, 5]. Later Vereninov achieved a closer match between theoretical and experimental types of analysis using Ussing's criterion of passive membrane transport [6].
By studying short-circuited to zero frog skin, Ussing and Zerahn found that the total current was equal to sodium flux; but when a potential difference was reappeared, the sodium flux decreased [7]. Mathematical description of this effect given by Ussing revealed a relationship between the unidirectional ionic flux ratio, the ratio of ion concentrations inside and outside skin, and the value of TP. By analyzing this relationship, it is possible to decide whether or not the membrane transport has an active component [8]. Thus, the analysis revealed the presence not only of active sodium pumping but also mainly passive iodide transport in frog skin [7, 8]. The first application of Ussing's criterion to analysis of cellular membrane transport was done on neurons [9].
Ussing further contributed to the elucidation of the mechanism of sodium transport in isolated frog skin by showing that both influx and efflux of 24Na is hyperbolically dependent on the external sodium concentration [10]. He called this mechanism “exchange diffusion”, which means coupled bidirectional movement of like ions. In 1959, Keynes and Swan, using the radioisotope method in the muscle suggested the existence in muscles of a specific sodium carrier. The carrier mechanism of the exchange diffusion was confirmed in experiments with the substitution of external NaCl by LiCl or choline chloride. The presence of a carrier can be inferred from the inhibition of 24Na efflux after the removal of external Na+. Sodium efflux in media containing 10 mM K+ has a hyperbolic dependence on sodium concentration when a fraction of sodium is replaced by lithium. The efflux rate decreased even more when potassium was excluded from the lithium Ringer's solution. The Michaelis constant for 24Na efflux was found to be 38 mM in a medium with 10 mM K+ [11]. Adrian and Slayman showed depolarization after ouabain treatment by measuring TP in Na-loaded muscles. The authors interpreted a decrease in TP by inhibition of electrogenic component of the Na+ efflux that was present in muscles with elevated Na+ concentration [12]. However, a reduction of TP by ouabain can be more accurately explained by a decrease in the electrochemical K+ gradient created by the sodium pump. Despite misconceptions about the particular mechanism of ion transport, these studies served as a methodological basis for analyzing ion fluxes and their role in bioelectrogenesis.
The first electrophysiological study of A. Vereninov was comparative and devoted to the application of a generalized strength-duration equation suggested by Nasonov and Rozental' [13]. The theoretical problem underlying this study was the choice between capacitance and diffusion mechanisms of excitation [2]. The use of invertebrate muscles for solving this problem was dictated by their longer stimulation time, which allows the determination of parameter n in equation i=a/tn+b. In this equation, the dimensionless parameter n varies from 0.5 (as in Nernst's diffusion equation) to 1 (as in the classical strength-duration equation). The values of n determined from the linear part of the strength-duration curves on a double logarithmic plot were 0.8 -0.9 in invertebrates and 1 in fibers of frog striated muscle or nerves. The latter value, however, was taken from other studies [2]. These data suggest the presence of the diffusion mechanism that is indicated by a lower n value [14]. However, longer stimulation time of invertebrate muscles indicates that t and n are not independent parameters, and therefore a lower n value cannot be used as an argument to support the diffusion hypothesis.
Initially, the concept of cell permeability was used for the explanation of the phenomenon of plasmolysis and de-plasmolysis in plant cells (see [1] for review). Later, this concept was applied to explain osmotic phenomena in erythrocytes and striated muscles. Experimentally, permeability was studied by measuring muscle volume in the presence of substances with different lipid solubility. The lipoid theory of Overton defined permeability as the ability of substances to penetrate lipid membranes. Overton predicted high permeability for urea based on its role as a waste product [15] or its effect on the contractility of muscles [16]. These mechanistic explanations marked the beginning of the modern membrane theory, which postulates the presence of pores and specific transport mechanisms. Contemporaries used data obtained by Overton for mechanical explanation of bioelectric phenomena. Thus, Höber used these data to explain the polarizing effect of monovalent cations on the muscle. However, he could not confirm the effects of calcium on muscle excitability [17].
Overton's statement about the low dissolving power of water for intracellular solutes met with criticism from both proponents and critics of the membrane theory. A. Hill determined osmotic pressure by measuring the vapor pressure of muscle and erythrocytes to test the presence of osmotically inactive water [18]. His statement that most water in muscles was in free state supported membrane theory while the finding that only half of water was osmotically active, as determined by traditional volume measurement, contradicted it. Hill explained this discrepancy by changing membrane permeability during prolonged treatment, which leads to the loss of potassium from muscles [18]. Nasonov and Aisenberg addressed the same problem, pointing to the role of non-electrolyte permeability. They found that adding 5 mM of egg albumin, 50 mM of dextran, 0.3 M of sucrose or 2 M of urea caused a 20% decrease in cell water content against the expected 50%. When expressing the concentration of added substances in volume percent, all these dependencies were in the same range. They concluded that volume changes in muscles are controlled by the colloid mechanism (see [1] for the review).
Bioelectric phenomena were a central point in both membrane and phase theories. In a series of experiments, Höber measured bioelectric potentials on the surface of muscles in presence of different cations and anions. He assumed that the potential difference (PD) between KCl-treated and untreated muscle parts is mainly determined by alkali cations while anions and divalent cations are less important [17]. The polarization effect of cations on the muscle membrane was specific and ranged for iodide salts in the order: K+ >> Rb+> NH4+ > Cs+ > Na+ > Li+. Due to the weakness of the lipoid theory, he used Bernstein's theory, which also focuses on the role of inorganic ions [19]. Since the effects of Rb+ and Cs+ do not fit within the theory, which assumes that permeability is determined by the radius of hydrated ion, Höber explained this disagreement by a hypothesis unrelated to the concept of membrane permeability. Among the factors responsible for this effect, he suggested the role of variations in the chemical activity of the protoplasm [17].
Nasonov and Alexandrov made further assumptions concerning the mechanism of ion activity changes. However, in contrast to the theory of Bernstein, they supposed that ions are released from their complexes with proteins during cellular activity. Thus, according to the phase theory, K+ diffuses from the altered zone to the intact part of the damaged muscle. This view contrasted with Bernstein's theory, where the injury-induced current arises between the internal and external faces of the membrane. Therefore, both theories only partially explain the complex bioelectric phenomena. To address these issues, A. Troshin proposed a mechanistic explanation of PD generation in the intact muscle. His explanation was based on two different phenomena – diffusion and sorption. Diffusion of ions occurred in the aqueous phase of protoplasm, while sorption occurred in the colloidal phase. Also, based on these phenomena, he constructed a model that successfully predicted the effect of inorganic ions on PD in intact muscle [1].
Historical view of a non-reductionist approach in Vereninov's studies
Vereninov's non-reductionist approach was developed in the classical physiological traditions. Wedensky’s and Nasonov's electrophysiological school had the most significant influence on this approach. Wedensky studied the generalized systemic response of nerves to stimulation during narcotic action [20]. He demonstrated that the optimum response was observed under intermediate stimulation of muscular preparation, while an increase and decrease in stimulation intensity led to a drop in the tetanus response. Treating these observations as separate phenomena, he combined them into one mechanistic concept of parabiosis. Parabiosis is a change in nerve conduction under intense stimulation, narcotics, and other non-specific factors [21]. Developing a similar concept of paranecrosis, Nasonov and Alexandrov studied the effect of sub-threshold stimuli on cells. Having found parallels between the processes of excitation and injury, they united it under one concept of paranecrosis (see [1] for review). Simultaneously, Russian physiologist E. Bauer gave a non-reductionist description of life phenomena, referring to mechanistic analogies rather than physical theories. Explaining the functioning of the living cell, he presupposed that it uses two types of work [22]. The internal work is done against equilibrium and transforms the free energy of substances outside the organism into the "structural energy" inside the organism. A second type of work is external, providing the stability of the whole system and thus participating in adapting the system to a changing environment. The mechanical analog of the first type of work is the work performed by a piston in an internal combustion engine. To explain the second type of work, he proposed the principle of "stable non-equilibrium". He theoretically analyzed this principle by considering proteins' function in enzymatic catalysis.Elements, including ions, are distributed within the cell highly heterogeneously [108]. First, we wish to point out that the presence of electric fields may compromise the accuracy or measurements of local ion concentrations using fluorescent probes, because the thermodynamic activity of the ion and possibly of the probe and/or the probe-ion complex will be affected by the same fields. The same reservations apply to electrode-based measurements. This potentially important practical question deserves further study. Atomic spectroscopy is a more direct way to quantify intracellular elements.
The non-reductionist approach can be demonstrated in experimental studies, where Vereninov examined the restoration of TP after depolarization caused by loading the muscle with KCl. In this study, he considered the variability of individual fibers. Variation of TP in muscles during recovery suggests the possible mechanisms that involve changes in potassium and chloride permeabilities [4]. In contrast, data usually obtained from molecular biology studies are not analyzed this way. Instead, biologists often use approaches based on model organisms that establish relations between the general characteristics of biological objects and the characteristics of a single organism. These approaches regard the organism as a model system for objects of the same or broader class even though they are quite specific in representation of their target [23]. Such models can also represent organs, tissues, and cells. However, the methodological and epistemic status of these models requires the use of other corresponding types of reduction. In experiments started in 1981, not included in this review, Vereninov mainly used cultured cells to study transmembrane ion fluxes. After 1990, his studies were carried out on rat thymocytes and human lymphocytes since the physiological parameters of these cells do not change significantly in vitro. Since 2004, the physiological parameters of the transformed myeloid cell line U937, which also served as a prototype of cancer cells, have been actively studied.
Using muscle as a model object presents methodological difficulties that can be solved mechanistically. The frog striated muscle can be separated into individual fibers representing the cellular level. A larger surface-to-volume ratio in the fibers compared to the whole muscle gives an advantage in the analysis of ion fluxes. For example, by measuring 42K+ fluxes during continuous fiber stimulation, Hodgkin and Horowicz calculated the amount of potassium transported during a single action potential [24]. Thus, although the entire sartorius muscle represents a more relevant object, isolated muscle fibers met the research needs in Vereninov’s early electrophysiological studies, especially since it was assumed that PD is generated inside the protoplasm.
Use of physical and mechanical models in study of “salt potentials”
Studies of “salt potentials” were originally done by Höber on injured muscles, but later he used intact muscles to test the membrane theory [17]. Boyle and Conway also used this method and found no meaningful difference between injured and intact muscle, provided that similar absolute changes in PD were observed with KCl addition to intact and injured muscles [25]. Also, using an intact muscle, Thoshin obtained the same order of cation selectivity as did Höber. However, in interpreting this order, Troshin assumed that it is due to specific interactions of ions with colloid particles and diffusion in the cytoplasm. This hypothesis was tested by measuring electric potentials in a complex coacervate system [1]. Troshin registered PD on the surface of solid coacervate consisting of gelatin and gum arabic. After the equilibration of coacervate with NaCl solution, one part of it was exposed to a test salt solution. The values of negative PD between the exposed and untreated part of coacervate ranged in the following order: K+ >Rb+ >NH4 +>Cs+ >Na+ >Li+ [1]. The obtained sequence was analogous to the dependence obtained in studies on muscles [17] but significantly different from those obtained with the same electrode system without coacervate [1]. In absence of coacervate the following sequence was obtained: Cs+ >Rb+ >K+ >NH4+ >Na+ >Li+ which corresponds to the diffusion of ions in the electrode system and is related to the radius of hydrated ions. These studies demonstrated the generation of PD in colloidal non-membranous system, imitating the properties of cytoplasm.
An acellular system that imitates phase properties of the muscle protoplasm was used by Vereninov to test the phase theory. The correlation between their physical properties was studied by locally applying a KCl solution to the surface of muscle fiber and a rod-shaped cation-selective material and measuring PD. To imitate longitudinal conductance that may compromise the value of salt potential generated by the membrane mechanism, the sample was made either solid or containing a long cavity filled with NaCl solution. The recorded PD between treated and untreated parts of the surface was not significantly affected by the presence of conductive NaCl solution within the cavity, suggesting the role of phase properties in its generation [26]. Thus, a physical model imitating the phase properties of a muscle demonstrated the role of specific ion sorption in the mechanism of PD generation. However, the data do not lead to an unambiguous choice between the phase and membrane theory of electrogenesis.
The non-reductionist modeling approach of Alexey Vereninov was clearly expressed in the construction of a model based on the cable properties of the muscle fiber. The choice of this model was dictated by the availability of an appropriate mathematical treatment and the ability to test its properties experimentally. According to R Taylor's cable theory, the decay of PD along the fiber follows the exponential law. This dependency can be measured in electrical circuits [27]. Therefore, the first part of the model is theoretical, used for explanation of the phenomenon while the second is predictive, used for “testing” of the underlying mechanisms. The testing was done using an electrical model constructed of resistive elements and voltage source. When applied in biological research, this mechanistic practice can be considered reductionist because it focuses on a particular mechanism. However, taken together with theoretical explanations it provides the most relevant way to analyze complex living systems. A similar approach can be found in an earlier study by Hodgkin and Keynes, who investigated potassium currents in nerve fibers [9].
Theoretical and mechanistic analytical aspects in Vereninov's study are closely connected. The modeling was performed using the following parameters: external longitudinal resistance re = 1300 kOhm/cm, internal longitudinal resistance ri =120 kOhm/cm, membrane resistance rm =51 kOhm*cm, and space constant λ= (rm/(re+ri))0.5 = 0.19 cm. Based on these parameters, resistor values were selected and used to construct a mechanistic model of the muscle fiber. Voltage was applied parallel to the rm resistor. The result of calculation matches the measured gradient of PD on the muscle fiber and distribution of the electric potentials on the resistor ladder network [27]. The excellent approximation of electric gradient on a muscle fiber by the cable equation confirmed the hypothesis of membrane mechanism of bioelectrogenesis. However, the changes in electrical gradient after adding or removal of KCl from the fiber surface suggest longitudinal diffusion of KCl within the fiber.
Thus, the generation of salt potentials depends on the transverse movement of ions, while their dissipation depends on longitudinal diffusion. Moreover, in interpreting these results, Vereninov did not exclude the participation of active transport and the movement of ions according to Donnan equilibrium. Testing of these possibilities became the main topic of his research since 1971. Meanwhile, in two studies discussed above Vereninov tested the effect of chloride on the “salt potentials”. He locally applied a solution with increasing concentrations of K+ and varying concentrations of Cl- to the surface of the muscle fiber. For that purpose, Cl- in solution was replaced with SO42-. He found a higher rate of generation and dissipation of the salt potential in Cl--free media [26]. In exploring this effect, he adhered to the point of view of the phase concept, according to which potassium acts by intracellular binding. This view contradicted Boyle and Conway's data that showed gradual changes in salt potentials caused by the addition of KCl to the medium [25]. By contrast, Vereninov’s view was supported by the data of Hodgkin and Horowicz showing that membrane potential of muscle fibers did not hyperpolarize upon potassium removal when chloride concentration in the medium was kept constant [28].
Mathematical modeling of TP in frog skeletal muscle
Vereninov developed an interest in mathematical modeling rather early in his career. His first theoretically oriented work, written together with T. A. Vinogradova was published in 1971. In that work, the authors considered a model of skeletal muscle membrane potential based on the assumption of passive distribution of ions between the muscle and external media [4]. As had been first shown by Boyle and Conway in 1941 [25], K+ is the major player in the generation of a negative TP, while chloride has a depolarizing effect. The depolarizing role of chloride was confirmed in a microelectrode study by Hodgkin and Horowicz [28] who loaded fibers with K+ and Cl- and incubated them in media with controlled Cl- concentrations. A decrease in the external K+ concentration did not lead to considerable changes in TP. That observation could not be explained by the membrane theory, and therefore, the authors postulated a non-Goldman type of K+ permeability, which later became known as "anomalous." The latter effect was further evaluated by Adrian [29]. By modeling the voltage-current relationships, he showed that depolarization (evidenced by high internal Cl-, according to the Goldman formula) is attenuated by outward K+ rectification.
The novel feature in Vereninov’s approach was the investigation of TP recovery by replacement of hypertonic Ringer solution with isotonic Ringer. It resulted in S-shape kinetics of repolarization, and the authors hypothesized that delayed K+ rectification was the reason. To prove this mechanism, extensive electrophysiological measurements on individual fibers would be required. However, as Vereninov and Vinogradova realized, the task could be significantly simplified if the experiments were supplemented by mathematical modeling. The algorithm used in their work was similar to that of Adrian [29] and additionally incorporated the data of Hodgkin and Horowicz [24, 28]. It allowed for the integration of ion fluxes in time, thus producing ion concentration dynamics [4]. This first mathematical model used by Vereninov was restricted to passive permeability, also called channel-like diffusion. This simplification permitted the computation of TP changes based on the Goldman equation [30, 31], and the model adequately described the long-term behavior of the volume and TP. In a later work, Vereninov extended this model to include the active ion transport term [32], which together with the Goldman leakage term became standard and was adopted by subsequent researchers [33, 34].
The mathematical model of ion transport based on the Goldman equation includes variable intracellular ion concentrations. Since ions contribute to osmolarity, the complete model should take into account the changes in cell volume. To better describe cell volume under realistic conditions, Vereninov included an additional parameter in the model - the total concentration of impermeable osmolytes in the medium. In this model, he developed the approach proposed by Boyle and Conway [25], who used a hypertonic KCl solution and assumed that K+ and Cl- move into the muscle until the osmotic balance with the medium is reached. By measuring dry and wet weight, both Adrian and Boyle and Conway [25, 29] found that muscle osmotically equilibrated in KCl and became swollen unless the external medium was hyperosmotic. But, as Vereninov pointed out, the stability of cell volume in hypertonic KCl solution contradicts the membrane theory while being consistent with the classical permeability concept of Nasonov and colleagues. This concept assumes that muscle is freely permeable to both ion species, so the electroneutrality of intracellular compartment is obeyed. Vereninov’s approach anticipated the modern understanding of muscle volume behavior, which incorporates both the classical permeability theory and specific membrane transport mechanisms [35, 36].
Modeling of TP changes in the frog skeletal muscle after addition of KCl
The data in Table 1 illustrate the successful application of Vereninov’s method in evaluating potassium and chloride permeabilities [4]. The Table lists the measured TP along with ion concentrations in the frog sartorius muscle. The ion concentrations were taken from other studies [29, 37]. In this study, muscles were first placed in Ringer solution supplemented with 100 mM KCl and then returned to normal Ringer buffer. The ratio of permeability coefficients for K+ and Cl- is found from the equation:
where the subscripts i and o denote the concentrations in the cytoplasm and the medium, respectively, U is the membrane potential, F is the Faraday constant, R is the gas constant, and T is the temperature. To find the absolute permeability coefficients from the PK/PCl ratio, Vereninov and Vinogradova made use of the Hodgkin and Horowicz result that PK varies in a wider range than PCl [28]. One limitation of Vereninov’s model was the neglect of volume changes upon KCl addition or removal.
In later modifications of the computational method, Vereninov corrected this shortcoming. The latest version of the program is available on https://vereninov.com/cellionfluxes/. The changes in media osmolarity are introduced there through parameter kv.
The parameter kv can be defined as the coefficient of proportionality between ion concentrations before and after cell volume change. In calculations that assume that the cell behaves as an ideal osmometer, internal osmolarity can be replaced by external ones. Vereninov suggested using this parameter in the study of lithium transport in U937 cells [38]. In subsequent studies, it was used to characterize osmotically induced changes [39, 40]. To demonstrate the role of kv in the changes of TP caused by the addition of 100 mM KCl to the medium, its value was set either to 1 or 1.8 and the calculations were carried out using a program for the computation of pump-leak flux balance in animal cells [41]. The rate of TP changes at kv = 1.8 is slower than at kv = 1.0 for all three permeability ratios (Fig. 1). These differences are not due to variations in absolute PK values since similar changes in kinetics were obtained using different PCl values. Also, for each ratio of permeability coefficients, lower TP values were obtained at kv = 1 (Fig. 1, black lines).
Vereninov and Yurinskaya demonstrated a similar hyperpolarizing effect of hyperosmotic treatment in an in silico study using experimentally determined characteristics of U937 cells [40]. Essentially, this effect appeared only at low PCl values, when the outward fluxes of K+ were higher than the outward fluxes of Cl-. In muscle, this effect is observed over a wider PK/PCl range, which is associated with low internal chloride concentrations. Thus, the hyperpolarizing effect of KCl at low PK/PCl values appeared only at the end of the incubation period (Fig. 1) when Cl- concentration rises to considerable level. Fig. 1 demonstrates the usefulness of kv for analyzing the changes in TP, especially at high PK/PCl values. The curve corresponding to high permeability ratio has an initial drop and immediate reversal (Fig. 1, black dotted line). This biphasic behavior is due to initial volume changes. If the calculation is performed for isosmotic conditions, i.e. by replacing 100 mM external Na+ with 100 mM K+ this feature is not observed unless unpermeant osmotic Bo is added to the external media. The best agreement between predicted data and microelectrode measurements is obtained at kv and the permeability coefficient ratio is set to 1 (Fig. 1, black dashed line). From the good match between this curve and the experimentally obtained value of -21 mV (Table 1), it follows that the effect of volume changes on TP is insignificant. However, considering the higher PK/PCl value obtained from TP values (Table 1), it is important to consider the initial volume changes.
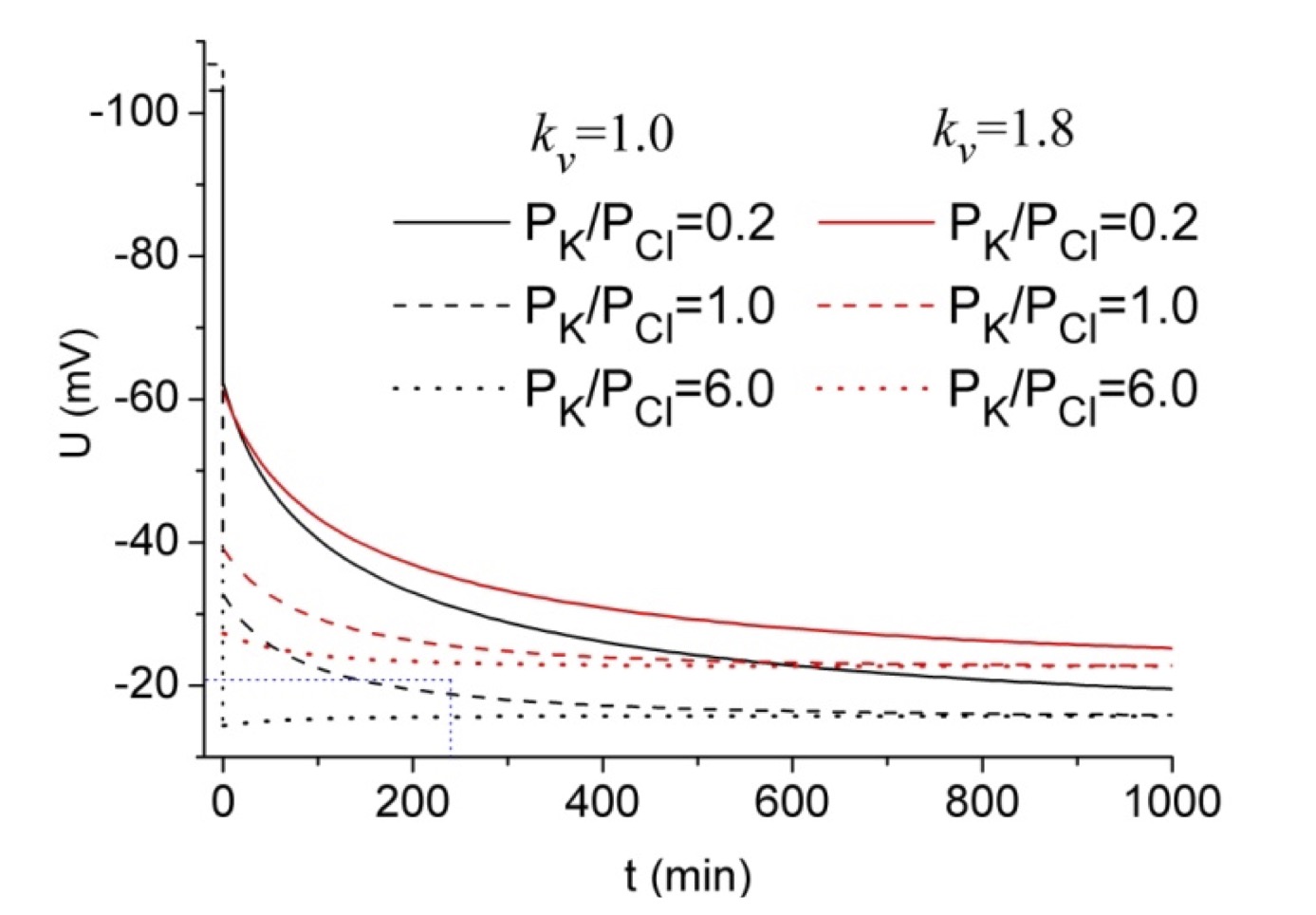
Figure 1. Changes of TP in a membrane Donnan system caused by the addition of 100 mM KCl to an external medium. Calculations were performed using the Web version of the program for the computation of pump-leak flux balance in animal cells [41]. The following initial parameters were used (in mM): [K]i =139, [Na]i =23.6, [Cl]i =3.8, [K]o =102, [Na]o =120, [Cl]o =221, PK was set to 0.002 min-1 (solid line), 0.01 min-1 (dashed line), or 0.06 min-1 (dotted line) while PCl was kept constant at 0.01 min-1. Parameter kv (the ratio of new to old osmotic strength after changing the medium) was set either to 1 (black lines) or to 1.8 (red lines). Parameters hp and tmax were set as appropriate. The values of all other parameters were set to zero. The initial values of TP (U) were calculated using the above settings except [K]o =2.5, [Cl]o =121. The vertical lines at zero time (t=0) represent the transition from the initial value to the first calculated value after changing the medium. The blue dotted lines highlighted the experimental value of TP obtained at 4 h.
Modeling of TP changes in KCl-loaded frog skeletal muscle after return to normal Ringer
Adrian in his modeling study estimated the dependence of voltage-current relationships on the internal Cl- concentration. The calculation of ion fluxes was performed in media with low external Cl- concentration when outward Cl- fluxes were dominant in the total membrane current. This was the condition at which the highest heterogeneity of repolarization was observed in real experiments [29]. It is known that Adrian carried out these experiments in solutions with constant osmotic pressure, which may also have influenced the scatter of the results. To test the effect of medium osmolarity on the kinetics of repolarization, Vereninov performed experiments in both isosmotic and anisosmotic conditions. When KCl-loaded muscles were placed in Ringer solutions with an additional 100 mM NaCl or 50 mM Na2SO4, the variability of electrical response was higher than in muscles returned to normal Ringer solution [4]. The disturbance caused by the osmotic factor suggests the presence of additional mechanisms making the repolarization response more complex. These mechanisms may be active ion transport or the effect of osmolarity on the PK/PCl ratio. The latter effect was considered by Vereninov in a modeling study assuming a normal Ringer solution as the external medium. In that study, he used experimental data of ion concentrations which stabilized after prolonged incubation in Ringer + 100 mM KCl (Table 1). As in the study described in the previous section, the PK/PCl values were altered by changing PK. The results of modeling at the PK/PCl = 1 closely approximated the experimental data obtained in a normal Ringer solution, while a decrease of PK/PCl led to a delay of repolarization [4].
Therefore, it would be interesting to test the effect of kv on repolarization kinetics. The results of calculations performed using the web version of the program at kv = 0.6 (Fig. 2) revealed an S-shaped repolarization kinetics obtained in the original study [4]. However, the current version of the program does not allow one to set kv to 1 under hyposmotic conditions. The reason for this difficulty was clarified in the study of I. Vereninov and co-authors [38]. They suggested that the reason for the program error is the excess of the internal osmolyte concentration over the external one. Another source of error is an exceedingly high value of TP. An alternative test for the effect of initial osmolarity change can be done by supplementing the medium with 100 mM NaCl, which is equivalent to setting kv to 1. Thus, as expected, no significant changes in the shape of the curves were observed in that study. Consequently, the kinetic of repolarization is independent of initial volume changes. Again, as in the study of Vereninov [4], a good agreement between calculated and experimental data was obtained at PK/PCl = 1 (Fig. 2, dashed line). The value obtained in modeling study approximates values calculated using Equation 1. Thus at the beginning of incubation and just before TP transients occurred, PK/PCl value is close to unity (Table 1). The original study also revealed sharp transient increases in PK that are responsible for S-shaped kinetics of repolarization. However, the mechanism of this increase remained unknown.
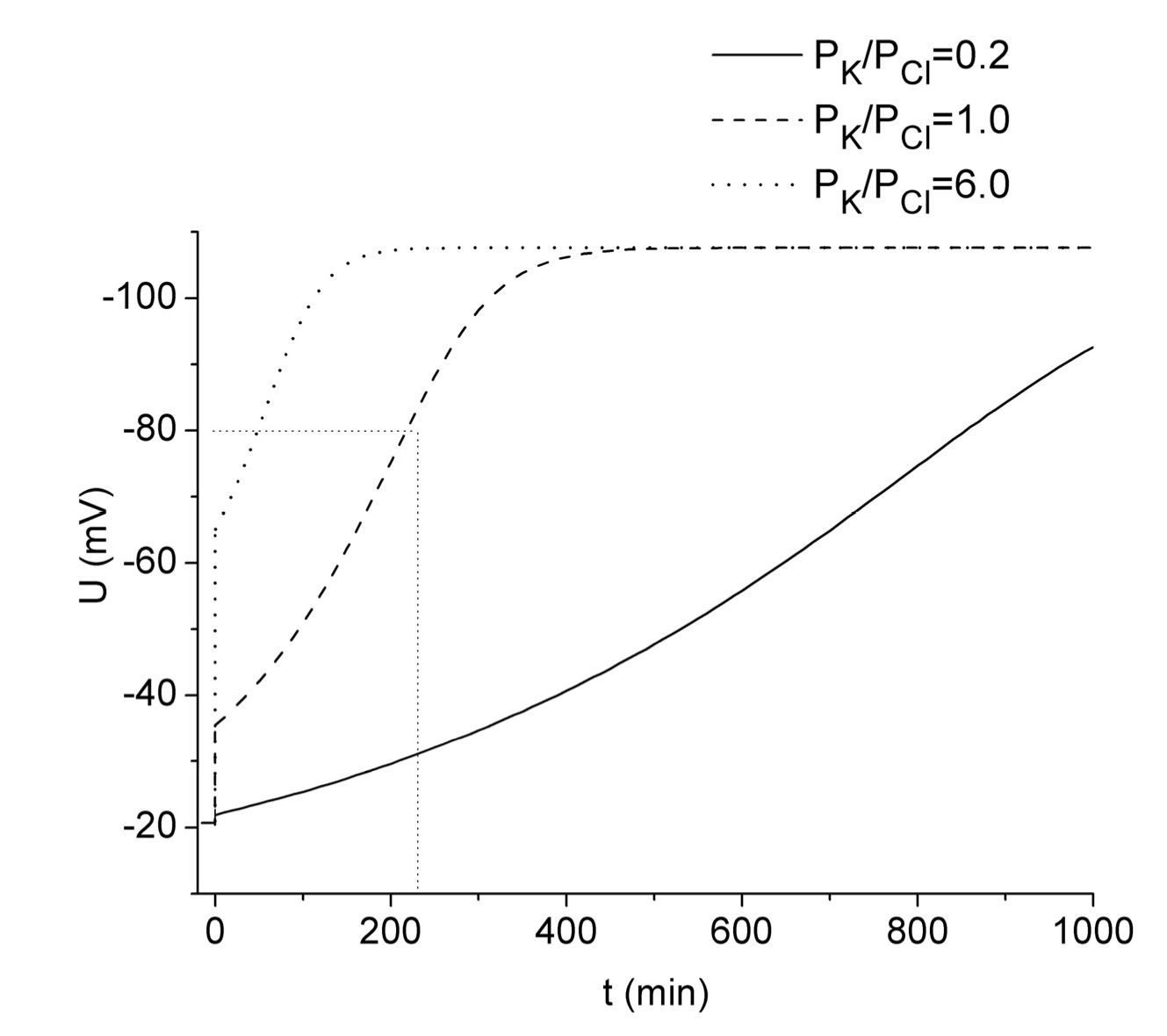
Figure 2. TP changes after the return of a Donnan system equilibrated with Ringer solution supplemented with 100 mM KCl to normal Ringer solution. Calculations were performed as in Figure 1 with the following initial parameters (in mM): [K]i =218, [Na]i =23.8, [Cl]i =102, [K]o =2.5, [Na]o =120, [Cl]o =121, kv = 0.6. PK was set to 0.002 min-1 (solid line), 0.01 min-1 (dashed line), or 0.06 min-1 (dotted line). The vertical lines at zero time represent the transition from the values of TP in depolarized muscles to the first calculated value after changing the medium. The values of TP in depolarized muscles were taken from the calculations in Figure 1 at a time point of 180 min. The small dotted lines highlighted the experimental value of TP obtained at 4 h.
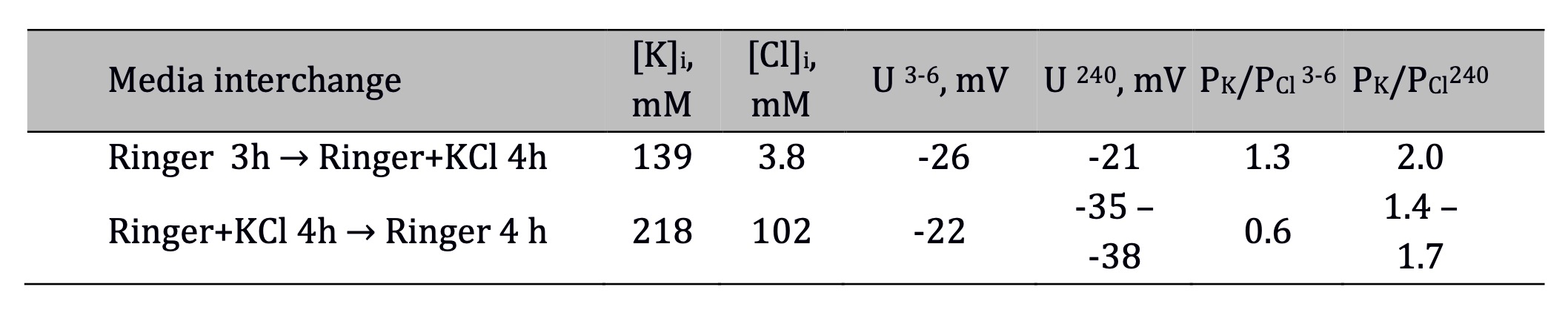
Table 1. Internal K+ and Cl- concentrations, TP and the ratio PK/PCl at the beginning and at the end of the incubation of muscles in Ringer solution supplemented with 100 mM KCl and after a return to normal Ringer solution. Values of [K]i and [Cl]i are taken from the studies [29] and [37]. The values of TP at the beginning and the end of the incubation period are taken from the original study [4]. The permeability ratios PK/PCl was calculated using Equation 1 at the beginning (3-6 min) and at 240 min of incubation. The calculated values are fully corresponding to values obtained in the original study. Data on repolarization in Ringer solution (second row) were obtained before the occurrence of TP transients. The Ringer solution consisted of ions in the following concentrations (mM): K+ 2.5, Na+ 120, Cl- 121, Ca2+ 1.8, H2PO4- 0.85, and HPO42- 2.15
The Goldman equation established the relationships between TP and the instantaneous values of unidirectional ion fluxes [30]. This equation was used in the modeling study by Vereninov and Vinogradova [4] for the calculation of TP generated by passive fluxes of K+ and Cl-. The effect of sodium in that study was minimized by the use of excessive amount of KCl. Another way to selectively study a particular transport pathway is to decrease the concentrations of interfering ion species. This approach, lowering the internal ion concentrations, was originally used by Overton [15] who treated muscles with hyposmotic saline or isosmotic sugar solutions. Later Harris and Steinbach further developed this approach by applying pure water or isotonic sugar solution to muscles and measuring the ion efflux rate. They found that fluxes of cations are electrically balanced by fluxes of anions [42]. The anion flux, however, may account for the anomalous dependence of TP on the external potassium concentration. Martirosov and Lev found considerable differences between measured and calculated values of TP when muscles were first exposed to a hyposmotic sucrose solution for 3 h and then incubated in various potassium-containing solutions for 15 min [43]. This method was applied by Vereninov in the study of the anomalous dependence of TP on potassium concentration [5, 44, 45].
Study of net potassium fluxes in K- and Na-depleted muscles
Martirosov and Lev used the Nernst diffusion equation for the theoretical assessment of TP [43]:
where aKo and aKi are potassium activities in the medium and in the cytoplasm. Using Equation 2, Lev calculated TP based on the measured ion concentrations and compared it to the experimental values of TP. They found that the formula overestimated TP in sucrose medium by 7 - 8 mV [43]. Martirosov and Lev explained the discrepancy by the absence of chloride in the external solution. Equation 2 is written in terms of activities instead of concentrations, but authors made no distinction between them.
Vereninov performed his studies under the same conditions as Martirosov and Lev but extended the second incubation by 6 h. By measuring the dry and wet weight at the beginning and the end of the incubation, he showed that water content decreased by about 30% in a medium with 2.5 mM K+ but remained unchanged in the presence of 75 mM K+ [44]. The intracellular potassium concentrations increased from 60 mM to 75 mM during incubation in a sucrose medium with 1.25 mM K2SO4 and from 60 mM to 65 mM in a medium with 38 mM K2SO4 (Table 2). For the calculation of TP, Vereninov used Equation 2 while based on concentrations. As shown in Table 2, the theory overestimated TP when medium contained 1.25 mM K2SO4, but underestimated it when concentration of K2SO4 increased to 38 mM. To explain these differences, the ratio of the influx to efflux rate constants was calculated using Equitation 3 derived from Ussing's equitation (Equation 5, see below):
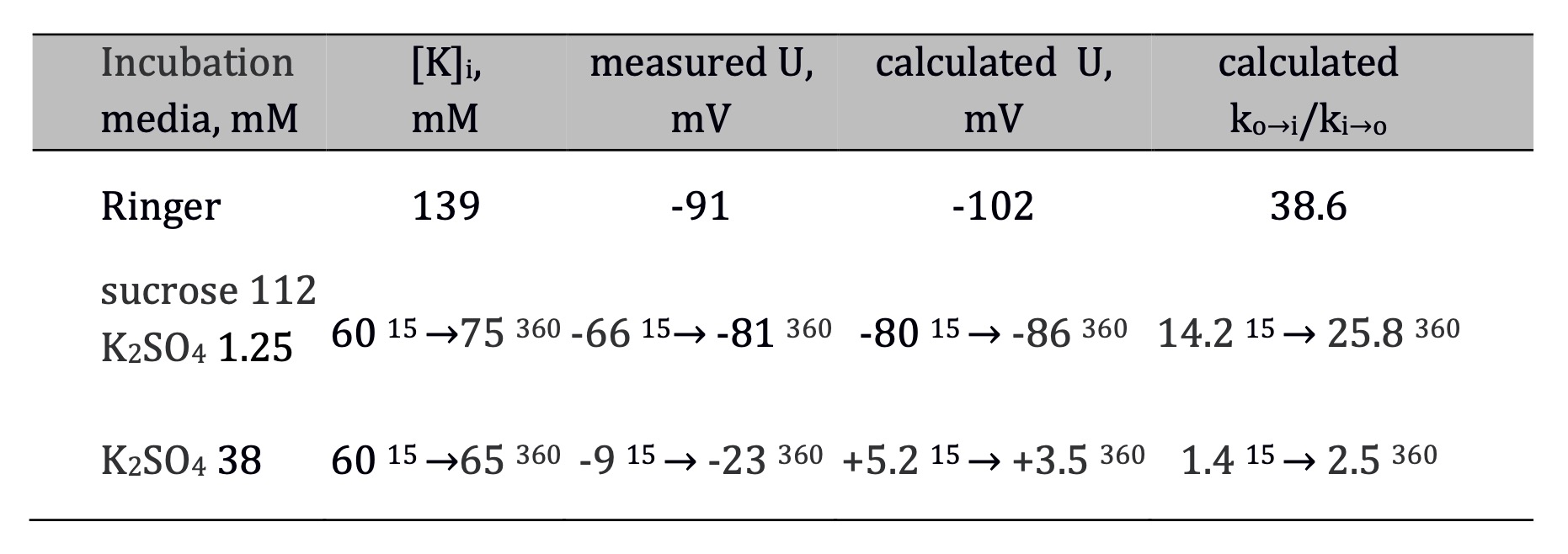
Table 2. Changes of internal concentrations of K+ ([K]i), TP, and the ratios of influx to efflux rate constants for 42K (ko→i/ki→o) during 6 h incubation in media with different K+ concentrations after equilibration in ion-free media (112 mM sucrose, 3 h). Media with 1.25 mM and 38 mM of K2SO4 additionally contained 8 mM CaSO4 and 1.5 mM K-phosphate buffer. The indexes indicate that the data were obtained at 15-minute and 360-minute incubation periods. The experimental values of [K]i and TP were obtained in original works [5, 45], with the exception of [K]i values in Ringer solution taken from [29]. The values of ko→i/ki→o were calculated using data in table and Equation 3
In that study, the analysis was done using a flux constant ratio and the difference between the calculated and measured values of TP at the beginning and end of incubation [5, 45]. The high ko→i/ki→o values in muscles incubated with 2.5 mM K+ suggested that K+ moves towards electrochemical equilibrium [5]. In the medium with 1.25 mM K2SO4, the difference between the theoretical and experimental values of TP during a 6 h incubation decreased. Furthermore, in the medium with 75 mM K+, the ratio ko→i/ki→o remained low, and the difference between the theoretical and experimental TP values increased at 6 h time point (Table 2). Therefore, the ratio ko→i/ki→o indicates the position of the system relative to the equilibrium state and thus characterizes the net ion movement. However, low flux constant ratio at 75 mM K+ may result from high bidirectional ion flux and does not reflect the absolute rate of ion flux. This phenomenon can be explained by the high rate of K+ self-exchange, which is electrically silent and can only be detected by the isotope method. This effect was considered in the later works of Vereninov. I. Vereninov and co-authors considered this problem using a program version designed for the study of coupled Li+ transport in U937 cells. They found that in normal conditions, coupled Na/Na and Cl/Cl fluxes constitute 70 and 90% of the corresponding overall turnover rate [38]. These studies demonstrate that analysis of net ion fluxes using the values of ko→i/ki→o requires caution until the full set of parameters is available. In this case, modeling is a reliable tool for analyzing the system since all the components are taken into account.
Testing the hypothesis of independent ion fluxes for bidirectional transport of Na and K
If a bi-ionic system consists of two cations and is little or not influenced by anions, TP can be estimated using the following equation [28]:
where the subscripts o and i indicate the concentrations in the cytoplasm and media, respectively, and α is permeability coefficient in muscles taken as 0.01. By using this equation and varying composition of external media, Martirosov and Lev estimated the effect of Na+ permeability on the value of TP. The calculated TP value (-64.0 mV) in hypotonic Na2SO4-containing media was consistent with that measured (-63.5±2.2 mV) and was lower than the -71.5 mV value calculated using Equation 2. The agreement between the numbers calculated from Equation 4 and experimental data indicated a predominantly passive distribution of ions in the system [43]. Vereninov and Toropova conducted a detailed study of Na+ and K+ transport under similar conditions using the methodology applied in previous study. TP was measured in fibers located on the same muscles as the ones used to calculate theoretical influx to efflux ratios [6]. This allowed discrimination between active and passive mechanisms of ion transport using Ussing's criterion of independence [8].
H. Ussing initially applied the independence criterion to distinguish between passive and active mechanisms of chloride transport [8] and sodium transport [7]. By applying this criterion to K+ passive distribution, the following equation was developed [9]:
where Mo→i and Mi→o are the inward and outward K+ fluxes, having units of μM K+ per g of dry weight per hour. This criterion assumes that the flux ratio is determined by the chemical gradient [K]o/[K]i and the value of TP. The following equations were used to replace ion fluxes with the flux rate constants that are more convenient for measurement [6]:
By substituting Equations 6 and 7 into Equation 5, Equation 3 can be obtained and used for the calculation of efflux and influx constant ratios (ko→i/ki→o).
Bidirectional fluxes for 86Rb were studied in muscles depleted of sodium and placed in sodium-free medium while 22Na fluxes studied in muscles placed in potassium-free media. The operation of the sodium pump stops under these experimental conditions. Although the bi-ionic system favors passive ion distribution, the difference between calculated and experimental ko→i/ki→o values for both ions suggests active transport. Moreover, inhibition of the 22Na efflux by ouabain suggests an active pump (Table 3). However, even in the presence of ouabain, 22Na flux constants did not provide unambiguous evidence for the independence of sodium transport [6]. This reasoning cannot be applied to 86Rb transport either, but available data allow deducing a mechanism that is not directly testable by Ussing's relation. It should be noted that the interference of Rb+ and K+ in bi-ionic system and the close similarity of these ions [12] do not account for this mechanism.
The experimentally determined ko→i/ki→o values in the K+ + Rb+ system were approximately 2-time lower than would be expected from passive distribution of K+ (Table 3). This fact may be interpreted as a coupled Rb/Rb electroneutral exchange. Although the exact mechanism of K/K exchange in muscles is unknown, it may be similar to Na/Na exchange, which occurs in muscles with high sodium content [11]. Also, K/K exchange operates in ATP-depleted erythrocytes, where it is catalyzed by the sodium pump [46]. The possibility of K/K exchange was discussed in this review in connection with data in Table 2 showing that the calculated ko→i/ki→o values for 42K fluxes in a medium with 75 mM K+ are lower compared to the 2.5 mM K+ medium. Data in Table 3 also confirm this fact for 86Rb. The decrease in ko→i/ki→o values is at least partially due to an overall increase in transport rates. Identifying the exact mechanisms of ion transport by using Ussing's criteria is impossible. However, mathematical modeling helps solve this problem, which was a matter of further research by Vereninov.
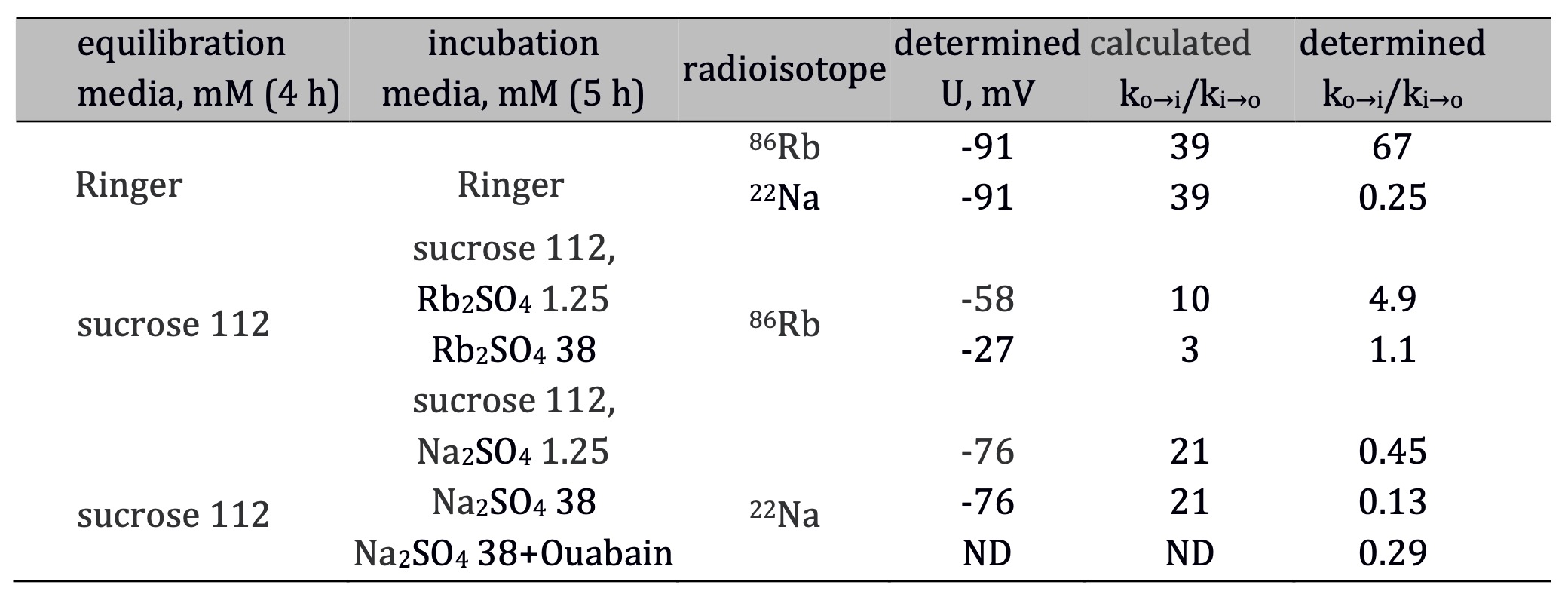
Table 3. The application of the Ussing criterion to distinguish between passive and active fluxes of Rb+ and Na+. Ratios of influx to efflux rate constants (ko→i/ki→o) were determined in muscles incubated in Ringer solution or equilibrated in K+-free sucrose media and transferred to the incubation media containing either 1.25 mM or 38 mM of Rb2SO4 or 1.25 and 38 mM of Na2SO4. Each of sulfate-containing media additionally contained 8 mM CaSO4 and 1.5 mM K+ phosphate buffer. Influx rate constants were determined at 83 min when muscles were loaded with 86Rb or 22Na. Efflux rate constants were determined after their transfer to isotope-free media. All data were obtained from the original study [6]
The non-reductionist modeling approach plays an important role in biological studies. Some of the most successful applications of this approach are found in the studies of cellular ion homeostasis; unlike other models that assume specific transport mechanisms, Vereninov’s approach only relies on experimentally measurable parameters, which allows it to solve problems more generally and makes model more flexible. His initial interest in passive ion transport in the frog striated muscle was dictated by theoretical consideration and its accessibility for experimentation. A muscle is an autonomous tissue that remains viable for a long time without external energy sources. For that reason, a muscle can maintain ion homeostasis; however, it may involve other mechanisms in this process. A modeling study conducted in 1971 fully validated the permeability values for two ions that were assumed to be passively transported. A later modeling study included active and other mechanisms of ion transport. Results calculated in the newest version of the program completely match the original data and suggest that the membrane transport system operates as a complex integrated mechanism that is described by a correspondent model. This type of model stands in contrast to simple mechanistic models used to represent particular mechanisms [47]. Mechanistic models may be called predictive because they explain (or predict) only an aspect of the phenomenon for which a particular mechanism is responsible. However, it is often challenging to separate mechanical and theoretical aspects in modeling. For example, Hodgkin and Huxley used the mechanism called “charged particles” in a model of nerve impulse propagation. In this model, charged particles describe both sodium permeability and the gating mechanism for sodium [48]. A simple mechanical model has also been used to test the “long channel” hypothesis, initially in the study of K+ efflux in giant axons [9].
In developing an integrated model, Vereninov combined theoretical and practical aspects of analysis. Initially, his research was concerned with the phenomenon of ion permeability, emphasizing the passive component of ion transport. His model was object-specific and restricted to a particular type of cells. At the same time, it may be considered non-reductionist similar to “model organisms” [23]. Later, he turned to problem-specific modeling, which has a reductionist purpose. The integrated modeling approach has a mechanistic basis and provides virtually unlimited possibilities for studying ion transport mechanisms. Therefore, the goal of this integrated approach is to offer as many of the system's parameters as possible. The main reason to qualify his early modeling studies as non-reductionist is their wealth of theoretical considerations. Although his model of ion transport was generally based on the same theoretical principles as those of others, the specific implementation of the modeling problem was quite original. One of the problems that Vereninov’s and other models have tackled is the influence of impermeant ions on the ionic and osmotic balance of the cell. Recently Model et al. (2023) examined the role of impermeant ions in electrolyte balance using four mathematical models, including Vereninov’s (https://vereninov.com/cellionfluxes/). Although all models used different methods for calculating changes in TP and ion concentrations, the obtained results were quantitatively and qualitatively similar [31]. In another work, Vereninov’s code has been used to identify the factor responsible for cell vacuolation under certain experimental conditions [49]. The code is currently being used for teaching human and animal physiology courses at Kent State University.
The authors are thankful to Dr. Vereninov I.A. and the students of the Peter the Great St-Petersburg Polytechnic University (St-Petersburg, Russia) for developing and supporting the website vereninov.com. The authors acknowledge M. Model, who initiated this study.
Author Contributions
AM fully contributed to the conception, design of the work, and the writing of the manuscript. J. Engohang-Ndong contributed to the first and the last versions of this manuscript.
Funding Sources
The research was carried out with funds of the Ministry of Science and Higher Education of the Russian Federation (state assignment № 124022600337-0).
Statement of Ethics
The authors have no ethical conflicts to disclose.
The authors have no conflicts of interest to declare