

Original Article - DOI:10.33594/000000602
Accepted 03 January 2023 - Published online 25 January 2023
1Department of Biomedical Engineering, Northwestern University, Evanston (IL), USA;
2Department of Neurobiology, Northwestern University, Evanston (IL), USA;
3Department of Ophthalmology, Northwestern University, Chicago (IL), USA
Background/Aims: For many years experimental and theoretical studies of the processes controlling the transmembrane potential of living cells and their volume were focused on ions, first of all Na+, K+, and Cl-, that can be moved in and out of the cell by various active and passive mechanisms. But recently more and more attention has been directed toward the internal impermeant anion (Xz-) – a complex entity that is comprised of many very different molecules. The most intriguing feature of the internal impermeant anion is that its amount and, importantly, its mean valence can be changed during the metabolic activity of the cell. The aim of this paper is to computationally investigate how changes in the amount and the mean valence of the internalimpermeant anion influence the concentration of the main ions, the membrane potential, and the cell volume. Methods: The computational analyses were performed using our charge-difference model describe earlier. Results and Conclusion: The results of computational simulations confirm previous results that changes in the amount of Xz- influence nothing but the cell volume if z remains constant, although transient disturbances of concentrations and Em happen and their extent depends on the speed of Xz- changes. Changes of z have more serious consequences. A decrease of |z| leads to a decrease of concentrations of cations ([K+]i and [Na+]i), to an increase of the concentrations of anions ([Cl-]I and [Xz-]i), and to depolarization of the cell membrane; an increase of |z| leads to changes in the opposite directions. Interestingly, even in conditions when Xz- remains unchanged, the normal electrophysiological activity expressed in changes of Em will affect [Cl-]i and consequently [Xz-]i (due to volume changes), inducing feedback effects on the cation concentrations and Em. Accordingly, Xz- is viewed as an important but not the only component of a broader concept of osmolarity-charge asymmetry. The basic physical reasons that determine the interrelations between Xz- on one hand and ionic concentrations, Em, and the cell volume on the other hand are discussed.
Among countless chemical components that fill a living cell and are present in the media surrounding it, there are four entities which are assumed to be particularly important for the cell volume and membrane potential regulation. Three of them are ions: two cations, Na+ and K+, and one anion, Cl-. Nonequilibrium transmembrane distribution of Na+ and K+, which is supported by a constant expenditure of energy (hundreds of millions of ATP per second for an average neuron), determines the negative membrane potential and serves as a basis for all systems of ionic homeostasis. Cl- transmembrane distribution depends mostly (entirely, in the absence of Cl-transporters) on the membrane potential, but the presence of significant Cl- membrane conductance makes possible (and even inevitable) the existence of osmotically imbalanced transmembrane ionic fluxes, which cause changes of the cell volume. Although there is undeniable importance of other ions (like Ca2+, Mg2+, HCO3-, PO43-), those three are mostly responsible for regulation of the cell volume and the membrane potential.
The fourth fundamental component of the volume-voltage regulation system is the so-called “internal impermeant anion”, Xz-. The complication with this “impermeant anion” is that it is a collection of very different molecules, large and small, electrically neutral and charged, both positively and negatively. It is often defined in computational papers as “everything that is inside of the cell except Na+, K+, and Cl-”. The label “impermeant anion” reflects two things which we know for certain: first, it consists of molecules which cannot leak through the plasma membrane of the cell, at least as fast as the main ions, and second, its net effect must be to act as an anion, i.e. the collective charge of this ensemble of various molecules should be negative to compensate for the deficiency of internal anions (since in every cell [K+]i + [Na+]i> [Cl-]i). The term “mean valence of impermeant anion”, z, characterizes how much of the electrical charge is carried by an average molecule of X, and is defined as the ratio of the total electrical charge of all molecules that together make X and the total osmolarity that they all create. The value of z, even though it is purely theoretical (there is no average molecule in the conglomerate of DNA, RNA, proteins, amino acids, nucleotides, mono- and polysaccharides, small inorganic molecules, etc.), is very important in determining how Xz- influences the cell volume-voltage system.
Various aspects concerning the internal impermeant osmolyte were touched on the previous publications [1-6], but the present work is entirely focused on computational investigation of the consequences that changes in the amount of X and its net valence z have on other ionic concentrations, the membrane potential, and the cell volume. The practically important questions about the composition of the ultracomplex item which is called “internal impermeant anion” and how changes of its components result in changes of its concentration and its mean valence is outside of the scope of this paper. Instead, it is focused on the net values of X and z and presents explanations about how and why changes of Xz- affect other main parameters of a living cell. It also will be shown why X and z should be viewed as parts of a broader concept of osmolarity-charge asymmetry.
The calculations were performed by our model described in detail earlier [1], but only the model capabilities needed for this work were used. For example, activity of the cation-Cl- cotransporters and the variable membrane permeability for water were not utilized. The explanation of the general strategy and approaches that were used during calculations follow.
Main parameters and their valuesThe model operates with these parameters:
Extracellular concentrations of Na+, K+, and Cl-
Intracellular concentrations of Na+, K+, and Cl-
Intracellular concentration of X and its mean valence z
Transmembrane conductances of Na+, K+, and Cl-
Activity of the 3Na+/2K+-ATPase, expressed as molecules of ATP used per sec
Other variables: Membrane potential (Em), cell volume
Capacitance of the cell membrane (constant).
Osmolarity of the extracellular solution in all simulations was 300 mOsm (mOsmoles/L) comprised of [Na+]o = 145 mM, [K+]o = 5 mM, [Cl-]o = 150 mM. The plasma membrane of the modeled cell had high water permeability, so the intracellular osmolarity was also 300 mOsm and any potential osmotic imbalance was immediately compensated by a water movement that led to appropriate changes in the cell volume.
The total transmembrane cation conductance of the modeled cell was 2e10 ions/(s*V), which corresponded to an input resistance of 312.5 MΩ; the ratio of cation conductances (gK+/gNa+) was different in different simulations (marked in the text). The conductance of Cl- (gCl-) was 1e10 ions/(s*V) in all simulations, except those in Fig. 1, where it was 0.
The cell volume was 1e-12 L at the beginning of all simulations. Some alterations of the cell parameters could lead to volume changes, which are presented in the text and the figures as percentages of the initial value. The capacitance of the cell membrane was constant (1.2e-11 F) and not affected by the volume changes, which were assumed to alter the geometrical shape of the cell leaving the membrane area unchanged.
Manipulations with X and z
For computational purposes the internal impermeant osmolyte Xz- consists of two parts: the charged osmolyte (Any- with the specific mean valence y) and the electrically neutral osmolyte (NeO).
Xz- = Any- + NeO; z = y*Any-/(Any-+NeO).
Separation of the neutral impermeant osmolyte from the total X gives the model an important flexibility. For instance, 60 mM of Xz- with mean valence z = -2 can be represented as (1) 30 mM of Any- with y = -4 plus 30 mM of NeO, or (2) 40 mM of Any- with y = -3 plus 20 mM of NeO, or (3) 60 mM of Any- with y = -2 and 0 mM of NeO; in all these cases we have 120 mM of negative charge and 60 mOsm of osmolarity. The amounts of Any- and NeO can be separately changed in time to produce any desirable changes of X and/or z.
Process of calculations
The model is based on charge-difference computational principles. There was no attempt to derive an equation that determines the membrane potential and the cell volume from ionic concentrations, their conductances, and activities of transporters. Instead, our program 1) counted transmembrane fluxes through the channels and transporters for each ion during a short time (1 msec in this work), during which the conditions are assumed to be unchanged, 2) calculated the resulting changes in intracellular ionic concentrations, osmolarity and electrical charge at the end of this time period, and 3) made appropriate adjustments of the intracellular concentrations, the membrane potential and the cell volume. After the cycle was complete, the results served as starting conditions for the next time step; this process was repeated for a predetermined time, for instance, 600, 000 times for 10 minutes. If a balanced (resting) state was reached, the combined fluxes through all appropriate channels and transporters for each ion (K+, Na+, and Cl-) would be equal to 0 and ionic concentrations, the membrane potential and the cell volume would not change. Changes in the conditions (a conductance, activity of the Na+/K+ pump, amount of internal impermeant osmolyte or its mean valence) disturb the balance, and a new balanced state should be found with potentially new values for the membrane potential and the cell volume, as well as for ionic concentrations. Consequently, at the end of the calculations the activity of the Na+/K+ pump, which depends on [Na+]i, could be different from its initial value.
When z is not equal to -1 (which is probably always), it creates a situation that we called “osmolarity-charge asymmetry”. Let’s see how the osmolarity-charge asymmetry influences internal ionic concentrations starting from an equilibrium state with no Na+/K+-ATPase activity and the plasma membrane permeable only to Na+and K+. We have 145 mM NaCl and 5 mM KCl outside of the cell. Inside the concentrations of cations are the same, but part of the Cl- is replaced by 60 mM of impermeant anion Xz- with z = -2, so that 30 mM of Cl- will be enough to compensate the electrical charge of the cations ([Cl-]i=[Na+]i+[K+]i-2*[X2-]i). But this system is not osmotically balanced, with 300 mOsm outside and 240 mOsm inside. In order to bring it to osmotic equilibrium, every intracellular concentration must be multiplied by 1.25 (or the cell volume decreased to 80% of its initial value). As a result, the internal concentrations will be: [K+]i = 6.25 mM, [Na+]i = 181.25 mM, [Cl-]i = 37.50 mM, and [X2-]i = 75.00 mM. The slightly uneven transmembrane distribution of Na+ and K+ leads to (and is compensated by) slightly negative Em (-5.96 mV, at 36.7o C), which is equal to the equilibrium (Nernst) potential for both cations. This is a true equilibrium state; it does not need energy to be supported indefinitely. This situation could be confused with Donnan equilibrium, but it is not: in the presence of Cl- conductance (which is a must for Donnan) the equilibrium will be broken, and the cell volume will increase until the cell blows up.
Now let the Na+/K+-ATPase redistribute Na+ and K+ starting from three different osmolarity-charge setups. In all these initial (no pump) configurations [Cl-]i was 30 mM and the remaining 120 mM of the negative charge needed for macro electro neutrality was carried by 240 mM of X0.5-, 120 mM of X1-, or 80 mM of X1.5-. Table 1 shows the initial intracellular concentrations (in mM) and Em (in mV) after adjustment for osmolarity.
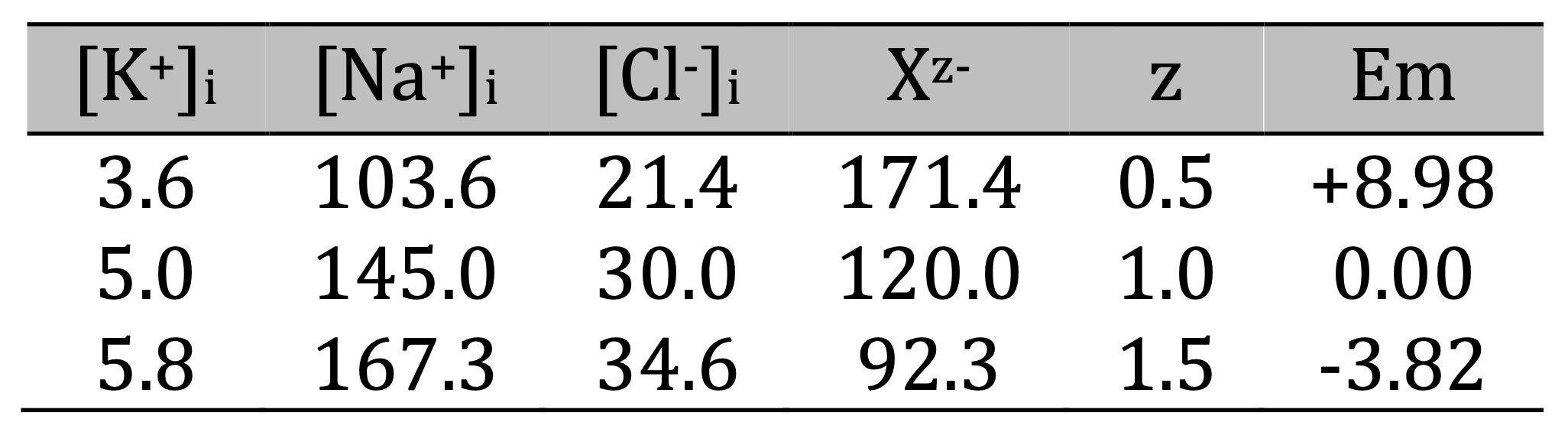
Table 1. Initial intracellular concentrations (in mM) and Em (in mV) after adjustment for osmolarity
Note that in this equilibrium (no pump) state Em was positive when |z| < 1, and negative when |z| > 1, due to decreased intracellular cation concentrations in the first case and increased intracellular cation concentrations in the second case.
Activation of the Na+/K+-pump results in replacement of intracellular Na+ with an equal amount of K+, regardless of the stoichiometry of the pump and the cation conductances, as was shown previously [1]. It leads to a thermodynamically imbalanced distribution of Na+ and K+ that must be supported by constant expenditure of energy. This expenditure must be large: 105 million ATP per second in the rightmost point of the graphs, i.e., 0.175 mM ATP per second in our modeled cell, would empty an ATP pool of 3 mM in less than 20 seconds if not constantly replenished by energy metabolism. The imbalanced distribution of Na+ and K+ is also accompanied by generation of negative Em, but practically does not affect the cell volume. The higher activity of the Na+/K+-pump, the stronger the cations’ transmembrane gradient, and the more negative Em. But the cation concentrations and the membrane potential also depend on the value of z (Fig. 1).
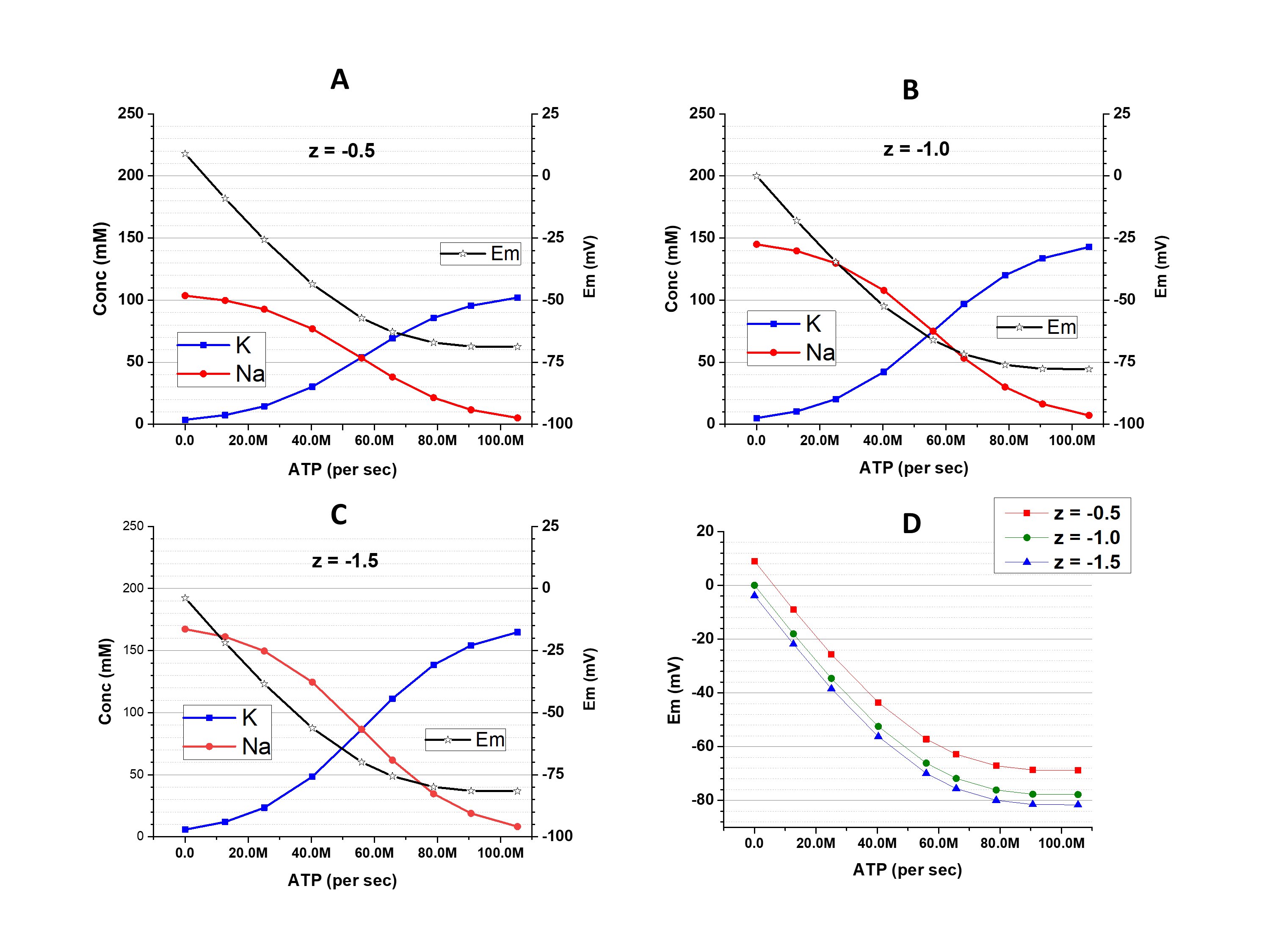
Figure 1. The [K+]i, [Na+]i, and Em at different activity of Na+/K+-pump and with different z. A: z = -0.5; B: z = -1.0; C: z = -1.5; D: comparison of Em dependence on the pump activity with different z. Note that in parts A, B, and C the left vertical axis is for the concentrations and the right vertical axis is for the voltage. The ratio gK+/gNa+ here (and in the series of simulations for the next Fig.) was 9 to produce stronger hyperpolarization. Importantly, gCl- was assumed to be 0 in this series. Here and in Fig. 2 the pump activities displayed in engineering notation with M for millions.
The main point illustrated in this series of calculations is that the z-dependent deviation of Em from 0 established in the no pump initial conditions is preserved in the whole range of pump activities. For instance, when z = -0.5, Em was 8.98 mV in the no pump state and was 8.98 mV more positive compared to z = -1.0 with all pump activities. When z = -1.5 Em was always more negative by -3.82 mV compared to z = -1.0. While the pump rate is the main determinant of Em, the value of Xz- has a consistent effect that is not negligible.
Importantly, in the above calculations gCl- was set to be 0 to keep the focus only on the cations. In next series of simulations, the calculations above were repeated, but with gCl- = 1e10 ions/(sec*V), which is a third of the total transmembrane conductance of the modelled cell.
When z = -1.0 (the osmolarity-charge symmetric condition because each average molecule of X is associated with one negative charge) the addition of gCl- has no effect on cation concentrations or Em, and the graph is identical to Fig. 1B; thus, it is omitted in Fig. 2. The changes of Em do have an effect on [Cl-]i: it is 76.3 mM in a slightly hyperpolarized (Em = -18.0 mV) condition with a pump activity of 12.7 million ATP per second (on the very left point of the graphs), but is decreased to 8.14 mM in a strongly hyperpolarized cell (Em = -77.8 mV) with a pump activity of 105.4 million ATP per second (on the very right point of the graphs). Changes of [Cl-]iare associated with the transmembrane movements of Cl- and also, due to requirements of the electroneutrality, the cations. Thus, the volume of the cell changes (163 % of the initial value with low pump and 84.6 % of the initial value with high pump). This, of course, has an effect on [Xz-].
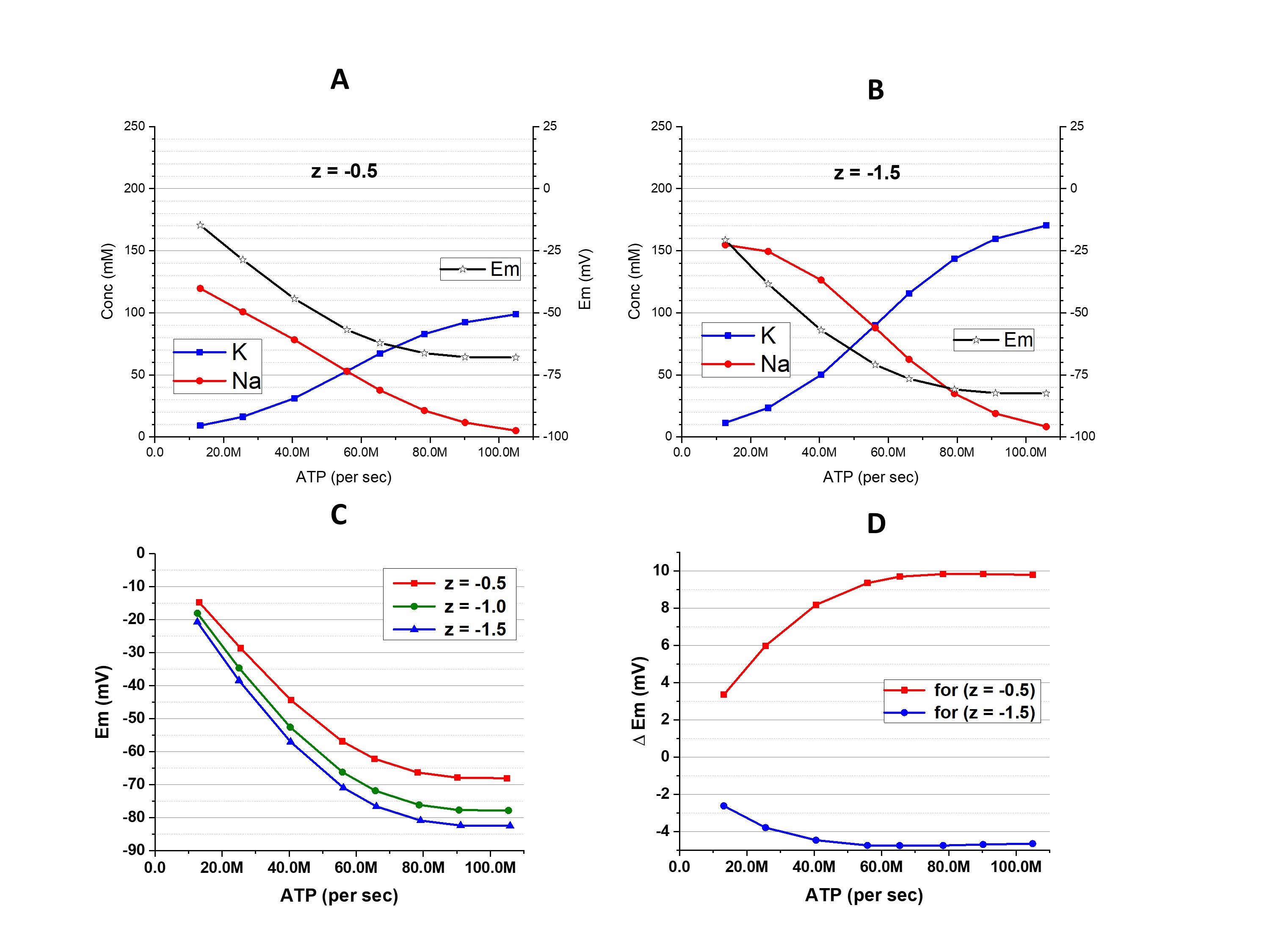
Figure 2. The [K+]i, [Na+]i, and Em at different activity of Na+/K+-pump and with different z. A: z = -0.5; B: z = -1.5; C: comparison of Em dependence on the pump activity with different z. D: the differences of Em obtained with z = -0.5 (red) and -1.5 (blue) from the Em obtained with z = -1.0. In contrast to Fig. 1, these results were obtained in a condition with substantial gCl-.
The situation is different when z ≠ -1 (osmolarity-charge asymmetric condition). A decrease of [Cl-]i dictated by the cation-dependent hyperpolarization is associated with an increase of [Xz-]. This leads to amplification of the osmolarity-charge asymmetry and a larger deviation of Em from osmolarity-charge symmetric conditions (Fig. 2, C and D). If |z| < 1 (like -0.5 in Fig 2A) the deviation has a positive sign, if |z| > 1 (like -1.5 in Fig 2B) the deviation has a negative sign. (Explanations in Discussion)
The conclusion of this part is that the changes of [Cl-]i, which are inevitable with changes of cation-determined Em, associate with changes of [Xz-] in the opposite direction. Shifts in the ratio [Cl-]i / [Xz-] influence the extent of the osmolarity-charge asymmetry that leads to alterations of [K+]i and [Na+]i and, in turn, Em.
As was shown above, a depolarization-induced increase of [Cl-]i must be accompanied by decrease of [Xz-]; in the case of hyperpolarization, [Cl-]i must decrease and [Xz-] increases. The opposite interrelation, in which primary changes of [Xz-] (due to, for instance, buildup during biosynthesis) could influence [Cl-]i , was also suggested [7]. But it was demonstrated computationally that buildup of Xz-, as well as a slow leak of Xz- out of cell, affects the cell volume and nothing else [1, 2, 6]. It should be noted that disturbance of the steady state during the buildup of Xz- temporarily affects ionic concentrations and Em (Fig. 3, A). As can be expected, the extent of the disturbance is dependent on the speed of the buildup (Fig. 3, B, C). But [K+]i, [Na+]i, [Cl-]i, [Xz-], and Em return to the initial values in a few minutes after ending the buildup.
Figure 3. Effects of buildup of Xz-. A: Disturbance of the cation concentrations and Em during 1 minute of fast buildup (0.12 mM/sec); B, C and D: Changes of Em, Xz- and the cell volume, respectively, evoked by buildups of different speed. In all cases an amount equivalent to 7.2 mM (in recalculation of the initial cell volume) of X-1.5 was added, in 1 minute, 10 minutes, or 10 hours. gK/gNa=4, gCl=1e10.
The only parameter affected by Xz- buildup was the cell volume. Xz- remains in the cell in all cases, but its concentration eventually returns to the initial value because volume increases proportionately to the speed of the buildup (Fig. 3, D). Volume finally reaches the same size since an equal amount of Xz- was added.
The previous simulation dealt with increasing of amount of Xz- that had a constant z. However, such changes hardly ever happen in real life. Different components of the internal impermeant anion can change with different rates when some others remain unchanged. Resulting changes in Xz- composition inevitably affect z. The following series of calculations will illustrate how changes of z associated with changes in Xz- will affect ionic concentrations, the membrane potential, and the cell volume. To simulate these changes, the internal impermeant osmolyte will be divided into two parts: electrically neutral (NeO) and charged (Any-), which has a specific mean valence y:
Xz- = NeO + Any-; z = y*Any-/(NeO + Any-).
In this series the specific mean valence y is always equal to -2. The changes in Xz- and z will be simulated by steady changes of NeO and/or Any- during an hour. In the initial rest state, the intracellular concentrations (in mM) and Em (in mV) were:
[K+]i 142.8, [Na+]i 7.2, [Cl-]i 8.1, [NeO]i 70.9, [An2-] 70.9, Em -77.8,
so [Xz-] = 141.8 mM and z = -1. To keep this system stable, 1.05e8 ATP per second was spent; gK/gNa = 9, and gCl = 1e10 ions/(sec*V). At time 0, An2- and/or NeO start to change to simulate 4 different scenarios:
1 – Amount of Xz- increased and |z| decreased due to buildup of NeO (0.03 mM/sec)
2 – Amount of Xz- increased and |z| increased due to buildup of An2- (0.01 mM/sec),
3 – Amount of Xz- was constant and |z| increased (+0.01 mM/sec of An2- and -0.01 mM/sec of NeO),
4 – Amount of Xz- decreased and |z| increased (+0.005 mM/sec of An2- and -0.015 mM/sec of NeO).
The resulting changes in concentration of Xz- and z are presented in Fig. 4.
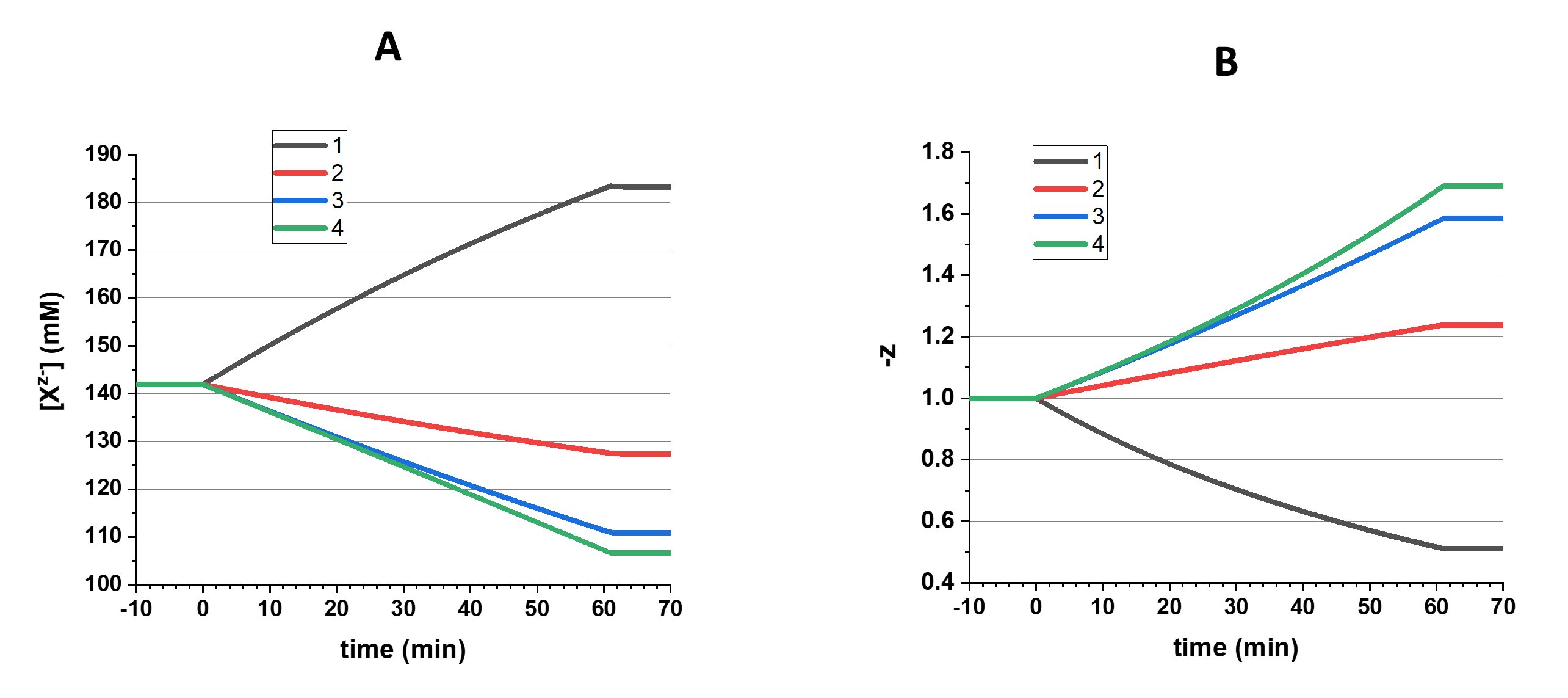
Figure 4. Changes in Xz- concentration (A) and z (B) in four different scenarios: 1 – amount of Xz- increases and |z| decreases, 2 – amount of Xz- increases and |z| increases, 3 – amount of Xz- remains the same and |z| increases, associated with increase of osmolarity, 4 - amount of Xz- remains the same and |z| increases, osmotically balanced. After a period of changes that lasts for 61 min, a 9 min period of stabilization is shown.
A few general notes should be made here. First, an addition of either NeO or An2- leads to an increase of Xz- amount, but in the first case z decreases because the charge is diluted (scenario 1) and in the second case z increases because the charge is concentrated (scenario 2). To increase z while the amount of Xz- remains unchanged (scenario 3), NeO is replaced by an equal amount of An2-. But for the sake of macro electroneutrality, the addition of two Na+ is required with each added An2-; that leads to an increase of the total amount of the osmotically active molecules. To avoid an increase of the internal osmolarity (scenario 4), the addition of Na+ is compensated by increased removal of NeO, but this results in a decrease of the amount of Xz-.
Then, the changes in amount of Xz- lead to changes in internal osmolarity and, consequently, the cell volume. As a result, the concentration of Xz- can decrease when the amount of it remains constant (scenario 3) or even increases (scenario 2; see Fig. 4).
Finally, it should be remembered that when we talk about increase of z it means an increase of its absolute value, ignoring the sign.
Effects of changes in amount of Xz- and z on ionic concentrations, Em, and the cell volume are shown in Fig. 5 for these same scenarios. In scenario 1 (upper row) the amount of Xz- is increasing because of buildup of its electrically neutral component, NeO. Not surprisingly, the cell volume also increases. But the elevation of the fraction of NeO in total Xz- diminish z, which is equal to -0.51 by the end of the buildup. More anions are needed for neutralization of the cations, and the concentrations of the former increase while the concentrations of the latter decrease. Decrease of both cation concentrations (although [Na+]i decreases only by 3.4%) results in depolarization of the cell membrane due to a reduction of the hyperpolarizing effect of K+ and an increase of the depolarizing effect of Na+. [Cl-]i is increasing following the depolarization.
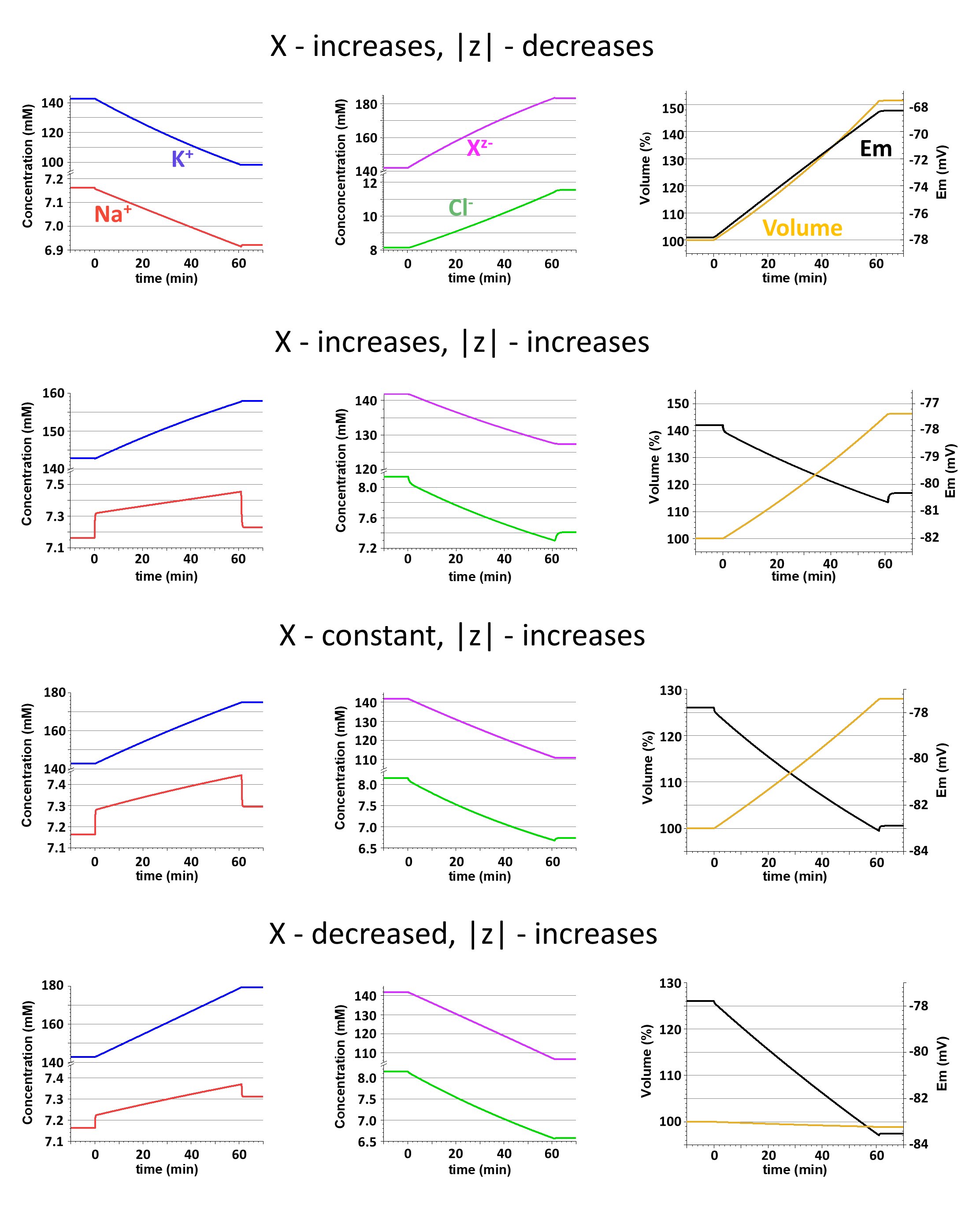
Figure 5. Consequences of changes in the amount of the internal impermeant anion (X) and in its mean valence (z) for cation concentration (the left column), anion concentration (the middle column), and volume and voltage (the right column). Each of four rows presents results of calculations in different scenarios associated with various changes in X and z. Detailed explanations are in the text. Note breaks in the concentration axis; the scaling above and below the breaks are different.
In scenario 2 (the second row in Fig. 5) the amount of Xz- is increasing because of buildup of its charged component, An2-, resulting in increase of z (-1.24 by the end of the buildup). Like in previous simulations, the cell volume increases, but the changes of the ionic concentrations and Em all go in opposite directions. This is understandable, since when [z]>1 fewer anions are needed to compensate for the positive charge of cations, so the anion concentrations decrease, and cation concentrations increase, producing a hyperpolarization. Among ionic changes, those of [Na+]i appear to be particularly interesting. The buildup of An2- (0.01 mM/sec) is accompanied by addition of Na+ (0.02 mM/sec) and it results in a relatively quick (in 30-35 seconds) initial increase of [Na+]i. Then the increase slowly continues. During the buildup [Na+]i is clearly out of balance (similarly to the disturbances illustrated in Fig. 3) and after the end of the buildup [Na+]i quickly decreases to a level that exceeds the pre-buildup value by only 1%. The dynamics of the [Na+]i increase are reflected in the time course of the hyperpolarization and, in turn, were copied by a decrease of [Cl-]i.
As expected, the increase in amount of Xz- from the two previous simulations leads to an increase in the cell volume. In scenario 3 (third row in Fig. 5) to avoid changes in the amount of Xz- the buildup of An2- is accompanied by simultaneously removing an equal amount of NeO. This results in an increase in z (-1.58 by the end of the buildup) and in all related changes in concentrations and voltage. There are some quantitative differences with results from scenario 2, but qualitatively they are similar, including the volume changes. In this case the volume increases because even when the amount of Xz- remains the same the total amount of osmotically active substances in the cell increases due to addition of two Na+ with each An2-.
In scenario 4 (bottom row in Fig. 5), to prevent a disturbance in osmolarity, addition of 0.005 mM/sec of An2- and 0.010 mM/sec of Na+ was balanced by removing 0.015 mM/sec of NeO. The stronger shift in Xz- toward the charged component results in a larger increase of z (-1.69 by the end of the buildup). All changes in concentrations and voltage are similar to those in the two previous cases, but volume remains almost the same. The slight decrease of the cell volume can be explained by a leakage of some Na+ that was out of balance during the changes of Xz- composition.
The model that was used in this work is undeniably simplified, operating with possibly the very minimum set of variables, but it permits a clear demonstration of some very basic interactions that could be obscured by the complexity of a more elaborate scheme. The focus was on one simple but fundamentally important fact that among the four entities that play the key roles in determining the membrane potential and the cell volume, three (Na+, K+, and Cl-) are monovalent, but the fourth (the internal impermeant anion, Xz-) is not. It leads to two important inequalities: first, the total concentration of internal cations is not equal to the total concentration of internal anions , and second, the total concentration of internal cations is not equal to the total concentration of external cations. We called this condition the osmolarity-charge asymmetry.
The equation for internal macro electroneutrality is:
[K+]i + [Na+]i = -z * [Xz-]i + [Cl-]i (1)
When |z| > 1, fewer anions are needed to electrically compensate the cations, and when |z| < 1, more anions are needed for this. The equation of osmotic balance is:
[K+]o + [Na+]o + [Cl-]o = [K+]i + [Na+]i + [Xz-]i + [Cl-]i (2)
The external cations make up exactly half of the external osmolarity, since
[K+]o + [Na+]o = [Cl-]o , (3)
But the sum of internal cations will be more or less than half the internal osmolarity (which is equal to external osmolarity) when |z| is larger or smaller than 1, respectively:
[K+]i + [Na+]i ≠ [Xz-]i + [Cl-]i (4)
As a result
[K+]i + [Na+]i ≠ [K+]o + [Na+]o (5)
The unequal transmembrane distribution of cations influences the membrane potential of the cell, slightly hyperpolarizing it when |z| >1 and depolarizing when |z| < 1. This membrane potential creates electrical forces that equilibrate the inequality of the cation concentrations across the membrane, and both Na+ and K+ are in stable equilibrium. Previously [1], the coefficient of osmolarity-charge asymmetry (k a ) was introduced to quantify these relationships:
k a = (-z * [Xz-]i + [Cl-]i ) / ([Xz-]i + [Cl-]i) (6)
and
[Na+]i / [Na+]o = 2 * k a / (k a + 1) (7)
[K+]i / [K+]o = 2 * k a / (k a + 1) ) (8)
Em = (RT/F) * ln (2 * k a / (k a + 1)) (9)
It should be remembered that while equations 1 to 6 are applicable in general, equations 7-9 are true only for an equilibrium state (no activity of the Na+/K+ pump) and in the conditions when the membrane is permeable only to cations. Addition of a Cl- conductance disrupts the equilibrium and makes it unattainable. Still, these equations are useful as they explain the link between the mean valence of impermeant internal anion, z, on one hand and cation concentrations and Em on the other. In reality, the activity of the Na+/K+ pump moves both Na+ and K+ out of equilibrium, but it always replaces internal Na+ with the same quantity of K+ (in the scale of macro electroneutrality) regardless of the stoichiometry of the pump and the cation conductances (see [1]). Accordingly, if the sum of Na+ and K+ inside the cell were different from the sum of Na+ and K+ outside (since |z| ≠ 1) in ideal equilibrium conditions, that difference will be preserved in the real nonequilibrium balanced state with the Na+/K+ pump at any level of activity. Em will deviate from what is expected with a certain pump activity and cation conductances by the same value as in the ideal equilibrium state (see Fig. 1, D). Thus, with help from equations 6-9 it is easy to predict how changes in z will affect ka and in turn the internal cation concentrations and Em.
It is also apparent from equation 6 that z is not the only factor that determines the extent of the osmolarity-charge asymmetry. The coefficient ka can be viewed as a mean valence of all internal anions, which dictates the cation/anion ratio inside the cell. In our simplified model the internal anions are only Cl- and Xz-. The larger the fraction of Cl- in the total internal anion, the closer ka to 1, and the smaller the Cl- fraction, the closer ka to z. Since the cell plasma membrane is permeable to Cl-, the internal Cl- concentration always follows the changes in Em. (In the presence of cation/Cl- cotransporters or other mechanisms capable of moving Cl- out of equilibrium, [Cl-]i still will increase with depolarization and will decrease with hyperpolarization of the membrane). When the changes of Em due to alteration of the Na+/K+ pump activity or a shift in gK+/gNa+ evoke changes in [Cl-]i this alters the extent of the osmolarity-charge asymmetry and in turn feeds back to affect the cation concentrations and Em (Fig. 2). This feedback is small in cells with low Em (and high [Cl-]i) and |z| close to 1, but begins to be more noticeable with hyperpolarization that lowers [Cl-]i and larger |z|.
One more factor that contributes to the osmolarity-charge asymmetry is the potential existence of electrically neutral osmolytes, both inside and outside of the cell. The internal impermeant neutral osmolytes can be viewed as components of Xz- (as done in this paper). But obviously the external neutral osmolyte cannot be treated this way. The concentration of the external neutral osmolytes is expected to be low (with possible exceptions in some special cases, like diabetes), but for the sake of accuracy the difference in concentrations of internal and external neutral osmolytes (d [osm]) should be added in equation 6:
k a = (-z * [Xz-]i + [Cl-]i ) / ([Xz-]i + [Cl-]i + d [osm]). (10)
An increase in concentration of external neutral osmolytes is equivalent to a decrease of the internal ones, and has the same effect on the osmolarity-charge asymmetry as an increase of |z|.
The shift in [Cl-]i enforced by changes of Em is associated with cell volume changes because the transmembrane flux of Cl- is tightly linked to co-directed fluxes of Na+and K+ by the demands of macro electroneutrality. And the volume changes, of course, affect the concentration of impermeant Xz-. For instance, depolarization-evoked increase of [Cl-]i leads to increase of the cell volume and decrease of [Xz-]i. It creates a wrong impression to say that Cl- is replacing (or in case of hyperpolarization is being replaced by) Xz-. In fact, the intracellular amount of Cl- (as well as amount of Na+ and K+) is changing; the amount of Xz- remains the same.
Another wrong impression is that relationships between [Cl-]i and [Xz-]i are reciprocal, i.e., changes [Xz-]i could produce compensatory changes in [Cl-]i. But [Cl-]i is fixed by Em, and changes in the amount of Xz- due to biosynthesis or biodegradation only affect the cell volume; the ionic concentrations, Em, and the concentration of Xz- itself remain unchanged [1, 2, 6]. However, this is only true in the case when z is constant. In reality, some of the components of the internal impermeant anion may experience changes when some others stay constant and that could affect not only amount of Xz-, but also its mean valance, z.
Changes of z have more serious consequences than changes of the amount of Xz- because they affect the extent of the osmolarity-charge asymmetry (see equations 6 and 10), and in turn ionic concentrations and Em. A decrease of |z| leads to a decrease of concentrations of both cations (the effect on [K+]i is much more prominent than the effect on [Na+]i , because K+ has larger internal concentration and higher transmembrane conductance), to an increase of the concentrations of both anions, [Cl-]i and [Xz-]i, and to depolarization of the cell membrane (the upper row in Fig. 5). An increase of |z| is associated with changes in the opposite directions: both cations increased, both anions decreased, and the membrane hyperpolarized. It should be emphasized that changes of z, not Xz- amount, determined the changes of [Xz-]i; the amount could increase, decrease, or stay unchanged, but the concentration would always decrease with elevation of |z| (2nd, 4th, and 3rd rows in Fig. 5).
The cell volume obviously depends on changes in the amount of Xz- but seems to be independent of z. Indeed, an increase of the amount of the charged component of Xz- and a decrease in the amount of its electrically neutral component both elevate |z|, but in the first case the cell volume increases while in the second case it decreases. However, it is not correct to assume that changes of z are irrelevant for the volume. Changes of z evoke the transmembrane redistribution of permeant Na+, K+, and Cl-, and as a result, during buildup of Xz- the cell volume grows slower than the Xz- amount when |z| is diminishing, but faster when |z| elevated. Accordingly, in the first case [Xz-]i is increasing but in the second it is decreasing (1st and 2nd rows in Fig. 5, respectively).
The composition of the internal impermeant osmolyte is complex and diverse, although it is possible to make an argument that phosphorus-containing molecules are dominant biological species in it (see Model et al. in this issue). Importantly, the composition is expected to change during the cell cycle with inevitable alterations in Xz- amount and the value of z. For instance, biosynthesis of the macromolecules (DNA, RNA, proteins) from the low molecular weight blocks (nucleotides, amino acids) is obviously associated with a decrease in the amount of Xz- but an increase of its mean valence z, since the total charge carried by the whole pool of internal impermeant osmolyte remans the same. The resulting effect will be an increase in the intracellular cation concentration (mostly K+) and membrane hyperpolarization, as in our scenario 4 (lowest row in Fig. 5). Dissociation of glycogen into glucose will increase the amount of Xz- and decrease z, diluting the charge; that will lead to a decrease in the cations and membrane depolarization, as in our scenario 1 (the top row in Fig. 5). In addition to redistribution between different components of the internal impermeable osmolyte its amount and the mean valence can be affected by the active transmembrane transport of small molecules. Such transport definitely takes place during, for example, cell growth. When an electrically neutral molecule (glucose) is transferred into the cell the effects will be similar to glycogen dissociation, but when the transferred molecule is charged (H2PO4-) the effect will depend on the current value of z. (In the case of the transmembrane transport, it should be remembered that most of the transporters are electrogenic and will directly influence the membrane potential.)
To summarize, although the membrane potential of the cell is determined mostly by the ratio of Na+ and K+ conductances and activity of the Na+/K+ pump, and the cell volume changes heavily depend on Cl- conductance, the roles of the internal impermeant anion, Xz-, and particularly its mean valence, z, should not be overlooked. Even in conditions when Xz- remains unchanged the normal electrophysiological activity expressed in changes of Em will affect [Cl-]i and consequently [Xz-]i (due to volume changes), modifying the extent of the osmolarity-charge asymmetry and inducing feedback effects on the cation concentrations and Em. On other hand, the metabolic activity in a cell, which is resting in an electrophysiological sense, can result in changes in Xz- and/or z that again influence the cation concentrations and Em. In certain conditions (low [Cl-]i in a strongly hyperpolarized cell and large |z|) this influence can be sufficient to induce a shift of Em in the range of 10 mV. As it was shown here, our program is capable of producing quantitative predictions on the changes in ionic concentrations, the membrane potential, and the cell volume based on knowledge about changes in the amount of internal impermeant osmolyte and its mean valence. The program with an explanation and tutorials is available for download from https://sites.northwestern.edu/ralcomputational/.
This article was inspired by works of Prof. Alexey Andreevich Vereninov, who was one of the first to point out particular features of the internal impermeant anion and its important role in the whole cellular ionic homeostasis.The work used the JAVA program designed by Alexander A Dmitriev.
Author Contributions
Andrey Dmitriev: Conceptualization, Investigation, Writing – original draft; Robert Linsenmeier: Writing – review and editing
Funding
The authors received no specific funding for this work
Statement of Ethics
The authors have no ethical conflicts to disclose.
The authors have no conflicts of interest to declare.
Dmitriev AV, Dmitriev AA, Linsenmeier RA: The logic of ionic homeostasis: Cations are for voltage, but not for volume. PLOS Comp 2019;15:e1006894.
https://doi.org/10.1371/journal.pcbi.1006894Düsterwald KM, Currin CB, Burman RJ, Akerman CJ, Kay AR, Raimondo JV: Biophysical models reveal the relative importance of transporter proteins and impermeant anions in chloride homeostasis. eLife 2018;7:e39575.
https://doi.org/10.7554/eLife.39575Vereninov IA, Yurinskaya VE, Model MA, Lang F, Vereninov AA: Computation of Pump-Leak Flux Balance in Animal Cells. Cellular Physiology and Biochemistry 2014;34:1812-1823.
https://doi.org/10.1159/000366382Model MA, Petruccelli J: Intracellular Macromolecules in Cell Volume Control and Methods of Their Quantification. Current topics in membranes 2018;81:237-289.
https://doi.org/10.1016/bs.ctm.2018.06.002Kay AR: How cells can control their size by pumping ions. Frontiers in cell and developmental biology 2017;5:41.
https://doi.org/10.3389/fcell.2017.00041Fraser JA, Huang CLH: A quantitative analysis of cell volume and resting potential determination and regulation in excitable cells. The Journal of physiology 2004;559:459-478.
https://doi.org/10.1113/jphysiol.2004.065706Glykys J, Dzhala V, Egawa K, Balena T, Saponjian Y, Kuchibhotla KV, Bacskai, BJ, Kahle KT, Zeuthen T, Staley KJ: Local impermeant anions establish the neuronal chloride concentration. Science 2014;343:670-675.
https://doi.org/10.1126/science.1245423